Giải Vở bài tập Toán 7 trang 129 Tập 2 Cánh diều

Với Giải VBT Toán 7 trang 129 Tập 2 trong Bài tập cuối chương 7 Vở bài tập Toán lớp 7 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VBT Toán 7 trang 129.

Giải VBT Toán 7 trang 129 Tập 2 Cánh diều

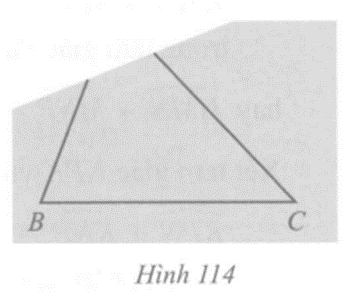
Câu 10 trang 129 vở bài tập Toán lớp 7 Tập 2: Bạn Hoa vẽ tam giác ABC lên tờ giấy sau đó cắt một phần tam giác ở phía góc A (Hình 114). Bạn Hoa đố bạn Hùng: Không vẽ điểm A, làm thế nào tìm được điểm D trên đường thẳng BC sao cho khoảng cách từ điểm D đến điểm A nhỏ nhất? Em hãy giúp Hùng tìm cách vẽ điểm D và giải thích cách làm của mình.

Lời giải:

Vì trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất nên khoảng cách từ điểm D đến điểm A là nhỏ nhất khi điểm D là hình chiếu của điểm A trên đường thẳng BC.

Suy ra AD là đường cao của tam giác ABC.

Vẽ hai đường cao BE và CK của tam giác ABC, hai đường cao đó cắt nhau tại H. Khi đó H là trực tâm của tam giác ABC. Suy ra D là hình chiếu của điểm H trên đường thẳng BC (Hình 115).

Câu 11 trang 129 vở bài tập Toán lớp 7 Tập 2: Cho tam giác MNP có $\hat{M}$ = 40^o, $\hat{N}$ = 70^o. Khi đó $\hat{P}$ bằng?

A. 10^o ;

B. 55^o ;

C. 70^o;

D. 110^o.

Lời giải:

Ta có $\hat{M}$ + $\hat{N}$ + $\hat{P}$ = 180^o (tổng ba góc của một tam giác).

Suy ra có $\hat{P}$ = 180^o – ( $\hat{M}$ + $\hat{N}$ ) = 180^o - (40^o + 70^o) = 70^o.

Vậy ta chọn đáp án C.

Lời giải Vở bài tập Toán 7 Bài tập cuối chương 7 Cánh diều hay khác:

• Giải VBT Toán 7 trang 123 Tập 2

• Giải VBT Toán 7 trang 124 Tập 2

• Giải VBT Toán 7 trang 125 Tập 2

• Giải VBT Toán 7 trang 126 Tập 2

• Giải VBT Toán 7 trang 127 Tập 2

• Giải VBT Toán 7 trang 128 Tập 2

• Giải VBT Toán 7 trang 130 Tập 2

• Giải VBT Toán 7 trang 131 Tập 2