Giải Vở thực hành Toán 7 trang 39 Tập 2 Chân trời sáng tạo
Với Giải VTH Toán 7 trang 39 Tập 2 trong Bài 2: Tam giác bằng nhau Vở thực hành Toán lớp 7 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 trang 39.
Giải VTH Toán 7 trang 39 Tập 2 Chân trời sáng tạo
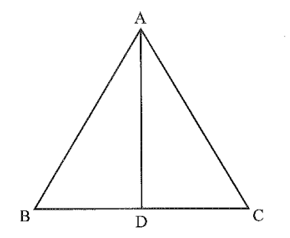
Bài 4 trang 39 Vở thực hành Toán 7 Tập 2: Cho tam giác ABC có AB = AC. Tia phân giác của góc A cắt BC tại D. Chứng minh rằng ∆ ABD = ∆ ACD.
Lời giải:
Xét ∆ ABD và ∆ ACD.
Theo giả thiết ta có: AB = AC; góc BAD = góc CAD;
AD là cạnh chung.
Vậy hai tam giác ABD và ACD bằng nhau theo trường hợp c.g.c.
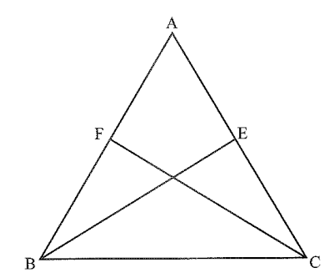
Bài 5 trang 39 Vở thực hành Toán 7 Tập 2: Cho tam giác ABC, có BE vuông góc với AC và CF vuông góc với AB. Cho biết góc FCB = góc EBC. Chứng minh góc ABC = góc ACB.
Lời giải:
Xét ∆ EBC vuông tại E và ∆ FCB vuông tại F.
Theo giả thiết ta có: góc FCB = góc EBC.
BC là cạnh chung.
Vậy, hai tam giác vuông EBC và FCB bằng nhau theo trường hợp cạnh huyền và một góc nhọn.
Suy ra, góc FBC = góc ECB hay góc ABC = góc ACB.
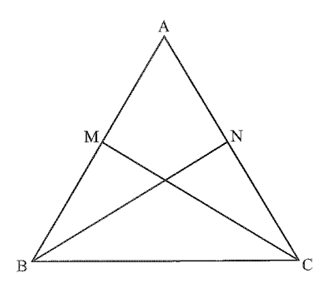
Bài 6 trang 39 Vở thực hành Toán 7 Tập 2: Cho tam giác ABC có BN vuông góc với AC và CM vuông góc với AB. Cho biết BM = CN. Chứng minh góc ABC = góc ACB.
Lời giải:
Xét ∆ NBC vuông tại N và ∆ MCB vuông tại M.
Theo giả thiết ta có: BM = CN.
BC là cạnh chung.
Vậy, hai tam giác vuông NBC và MCB bằng nhau theo trường hợp cạnh huyền và một cạnh góc vuông.
Suy ra, góc NCB = góc MBC hay góc ACB = góc ABC.
Lời giải Vở thực hành Toán 7 Bài 2: Tam giác bằng nhau Chân trời sáng tạo hay khác: