Giải Vở thực hành Toán 7 trang 40 Tập 2 Chân trời sáng tạo
Với Giải VTH Toán 7 trang 40 Tập 2 trong Bài 2: Tam giác bằng nhau Vở thực hành Toán lớp 7 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 trang 40.
Giải VTH Toán 7 trang 40 Tập 2 Chân trời sáng tạo
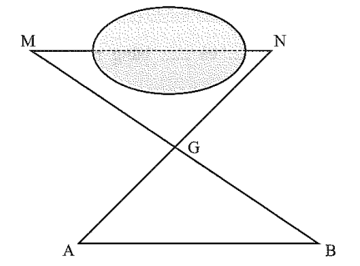
Bài 7 trang 40 Vở thực hành Toán 7 Tập 2: Để đo khoảng cách giữa hai cột mốc M, N ngang qua hồ nước, người ta chọn một điểm G sao cho đường thẳng GM và GN đều ở bên ngoài hồ, rồi lấy hai điểm A, B sao cho G là trung điểm của AN và BM ( như hình vẽ). Chứng minh AB = MN.
Lời giải:
Xét ∆ GMN và ∆ GBA.
Theo giả thiết ta có: GM = GB; GN = GA.
Góc MGN = góc BGA ( hai góc đối đỉnh).
Vậy, hai tam giác GMN và GBA bằng nhau theo trường hợp c.g.c.
Suy ra AB = MN.
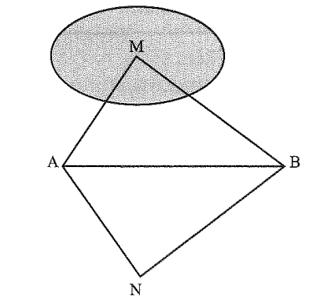
Bài 8 trang 40 Vở thực hành Toán 7 Tập 2: Để đo khoảng cách từ hai điểm A, B đến mốc M trên hồ, người ta lấy điểm N sao cho góc ABM bằng góc ABN; góc BAM bằng góc BAN (xem hình). Chứng minh MA = NA; MB = NB.
Lời giải:
Xét ∆ MAB và ∆ NAB.
Theo giả thiết ta có: góc ABM = góc ABN và góc BAM = góc BAN.
AB là cạnh chung.
Vậy, hai tam giác MAB và NAB bằng nhau theo trường hợp g.c.g.
Suy ra MA = NA; MB = NB.
Lời giải Vở thực hành Toán 7 Bài 2: Tam giác bằng nhau Chân trời sáng tạo hay khác: