Giải Vở thực hành Toán 7 trang 59 Tập 2 Chân trời sáng tạo
Với Giải VTH Toán 7 trang 59 Tập 2 trong Bài 8: Tính chất ba đường cao của tam giác Vở thực hành Toán lớp 7 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 trang 59.
Giải VTH Toán 7 trang 59 Tập 2 Chân trời sáng tạo
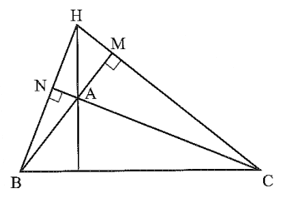
Bài 6 trang 59 Vở thực hành Toán 7 Tập 2: Cho ABC là tam giác có góc A > 90°. Hai đường cao BM và CN của tam giác cắt nhau tại H. Chứng minh AH vuông góc với BC.
Lời giải:
Vì ba đường cao của tam giác giao nhau tại một điểm nên giao điểm H của hai đường cao BM và CN cũng thuộc đường cao thứ ba.
Vậy AH vuông góc với BC.
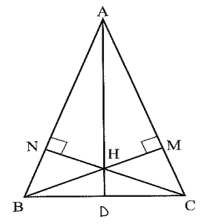
Bài 7 trang 59 Vở thực hành Toán 7 Tập 2: Hai đường cao BM và CN của tam giác nhọn ABC cân tại A cắt nhau ở H. Chứng minh đường thẳng AH đi qua trung điểm của BC.
Lời giải:
Vì ba đường cao giao nhau tại một điểm nên AH vuông góc với BC.
Gọi D là giao điểm của AH với BC.
Xét tam giác ADB vuông tại D và tam giác ADC vuông tại D.
AB = AC ( do tam giác ABC cân tại A).
Cạnh chung AD.
Vậy tam giác ADB bằng tam giác ADC theo trường hợp cạnh huyền – cạnh góc vuông.
Suy ra BD = CD. Như vậy D là trung điểm của BC hay đường thẳng AH đi qua trung điểm của BC.
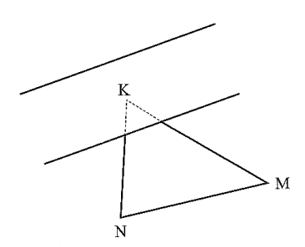
Bài 8 trang 59 Vở thực hành Toán 7 Tập 2: Điểm K ở giữa sông, hai điểm M, N ở trên bờ như hình vẽ. Muốn tìm điểm D, sao cho KD là khoảng cách ngắn nhất từ điểm K tới đường thẳng MN ta làm thế nào?
Lời giải:
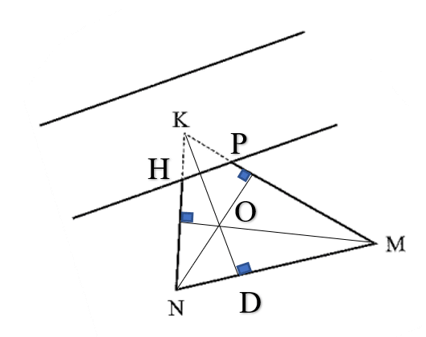
KD là khoảng cách ngắn nhất từ K đến MN khi KD là đường cao hạ từ K xuống đường thẳng chứa cạnh MN hay D là chân đường cao hạ từ K xuống MN.
Gọi giao điểm của NK và bờ sông là H, của MK và bờ sông là P.
Từ M kẻ đường vuông góc với HN, từ N kẻ đường vuông góc với MP. Hai đường vuông góc này cắt nhau tại O. Suy ra O là giao 3 đường cao của tam giác OMN. ( tính chất ba đường cao của tam giác)
Từ O kẻ đường thẳng vuông góc với MN. Đường thẳng vuông góc đó cắt MN tại D. Ta xác định được điểm D.
Lời giải Vở thực hành Toán 7 Bài 8: Tính chất ba đường cao của tam giác Chân trời sáng tạo hay khác: