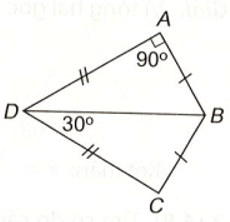
Cho các điểm A, B, C, D như hình vẽ bên. Chứng minh rằng ∆ABD = ∆CDB

Cho các điểm A, B, C, D như hình vẽ bên.

Giải Vở thực hành Toán 7 Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác

Bài 3 (4.6) trang 59 vở thực hành Toán lớp 7 Tập 1: Cho các điểm A, B, C, D như hình vẽ bên.

a) Chứng minh rằng $\Delta AB\text{D}=\Delta CB\text{D}.$

b) Tính $\widehat{ABC}.$

Lời giải:

a) Hai tam giác ABD và tam giác CBD có:

AB = BC (theo giả thiết).

AD = CD (theo giả thiết)

BD chung.

Do đó ∆ABD = ∆CBD (c – c – c).

b) Vì ∆ABD = ∆CBD nên $\widehat{A\text{D}B}=\widehat{C\text{D}B}=30°$ (2 góc tương ứng).

Do tổng ba góc trong tam giác ABD bằng 180° nên ta có

$\widehat{A\text{D}B}+\widehat{ABD}+\hat{A}=180°$

$\Rightarrow \widehat{ABD}=180°-\widehat{A\text{D}B}-\hat{A}=180°-30°-90°=60°$

Lại vì ∆ABD = ∆CBD, suy ra $\widehat{CBD}=\widehat{ABD}=60°$ (2 góc tương ứng).

Từ đây ta được: $\widehat{ABC}=\widehat{AB\text{D}}+\widehat{CB\text{D}}=60°+60°=120°.$