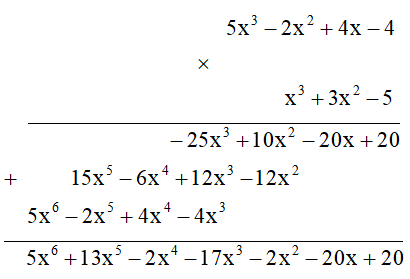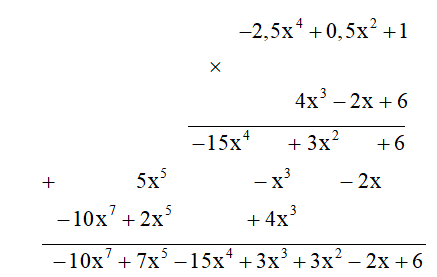Giải Vở thực hành Toán 7 trang 43 Tập 2 Kết nối tri thức

---

Với Giải VTH Toán 7 trang 43 Tập 2 trong Bài 27: Phép nhân đa thức một biến Vở thực hành Toán lớp 7 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 trang 43.

Giải Vở thực hành Toán 7 trang 43 Tập 2 Kết nối tri thức

Bài 6 (7.28) trang 43 vở thực hành Toán lớp 7 Tập 2: Thực hiện các phép nhân hai đa thức sau:

a) 5x³ - 2x² + 4x - 4 và x³ + 3x² - 5;

b) -2,5x⁴ + 0,5x² + 1 và 4x³ - 2x + 6.

Lời giải:

a) Ta đặt tính nhân như sau:

b) Ta đặt tính nhân như sau:

Bài 7 (7.29) trang 43 vở thực hành Toán lớp 7 Tập 2: Người ta dùng những chiếc cọc để rào một mảnh vườn hình chữ nhật sao cho mỗi góc vườn đều có một chiếc cọc và hai cọc liên tiếp cắm cách nhau 0,1 m. Biết rằng số cọc dùng để rào hết chiều dài của vườn nhiều hơn số cọc dùng để rào hết chiều rộng là 20 chiếc. Gọi số cọc dùng để rào hết chiều rộng là x. Tìm đa thức biểu thị diện tích của mảnh vườn đó.

Lời giải:

Số cọc dùng để rào hết chiều rộng là x (chiếc), suy ra số cọc dùng để rào hết chiều dài là x + 20 chiếc. Từ đó suy ra chiều rộng mảnh vườn là 0,1. (x - 1) (m), và chiều dài mảnh vườn là 0,1. (x + 19) (m).

Vậy diện tích của mảnh vườn là 0,1. (x - 1). 0,1. (x + 19) (m²). Thu gọn biểu thức này ta được:

0,1. (x - 1). 0,1. (x + 19)  = 0,01 . (x - 1)(x + 19)

= 0,01. (x² + 19x - x - 19) = 0,01. (x² + 18x - 19) = 0,01x² + 0,18x - 0,19.

Đa thức biểu thị diện tích mảnh vườn là S = 0,01x² + 0,18x - 0,19.

Bài 8 trang 43 vở thực hành Toán lớp 7 Tập 2: Rút gọn các biểu thức sau:

a) A = (2x² – 3x + 1)(x² – 5) – (x² – x)(2x² – x – 10);

b) B = (x – 2)(x² – 5x + 7) – (x² – 3x)(x – 4) – 5(x – 2).

Lời giải:

a) Đặt C = (2x² – 3x + 1)(x² – 5) và D = (x² – x)(2x² – x – 10), ta có A = C – D.

Trước hết ta tính:

C = (2x² – 3x + 1)(x² – 5)

   = (2x² – 3x + 1) . x² – (2x² – 3x + 1) . 5

   = (2x⁴ – 3x³ + x²) – (10x² – 15x + 5)

   = 2x⁴ – 3x³ + x² – 10x² + 15x – 5

   = 2x⁴ – 3x³ – 9x² + 15x – 5

D = (x² – x)(2x² – x – 10)

   = x²(2x² – x – 10) – x(2x² – x – 10)

   = (2x⁴ – x³ – 10x²) – (2x³ – x² – 10x)

   = 2x⁴ + (– x³ – 2x³) + (– 10x² + x²) + 10x

   = 2x⁴ – 3x³ – 9x² + 10x

Từ đó: A = C – D = (2x⁴ – 3x³ – 9x² + 15x – 5) – (2x⁴ – 3x³ – 9x² + 10x)

                             = (2x⁴ – 2x⁴) + (– 3x³ + 3x³) + (– 9x² + 9x²) + (15x – 10x) – 5

                             = 5x – 5

b) Đặt E = (x – 2)(x² – 5x + 7) và F = (x² – 3x)(x – 4), ta có B = E – F – 5(x – 2).

Trước hết ta tính:

E = (x – 2)(x² – 5x + 7) = x(x² – 5x + 7) – 2(x² – 5x + 7)

= (x³ – 5x² + 7x) – (2x² – 10x + 14)

= x³ + (– 5x² – 2x²) + (7x + 10x) – 14

= x³ – 7x² + 17x – 14

F = (x² – 3x)(x – 4) = x²(x – 4) – 3x(x – 4)

= (x³ – 4x²) – (3x² – 12x)

= x³ + (– 4x² – 3x²) + 12x

= x³ – 7x² + 12x

Cuối cùng ta được:

B = E – F – 5(x – 2) = (x³ – 7x² + 17x – 14) – (x³ – 7x² + 12x) – 5(x – 2)

= x³ – 7x² + 17x – 14 – x³ + 7x² – 12x – 5x + 10

= (x³ – x³) + (– 7x² + 7x²) + (17x – 12x – 5x) + (10 – 14)

= – 4.

Lời giải Vở thực hành Toán lớp 7 Bài 27: Phép nhân đa thức một biến Kết nối tri thức hay khác:

• Giải VTH Toán 7 trang 40 Tập 2
• Giải VTH Toán 7 trang 41 Tập 2
• Giải VTH Toán 7 trang 42 Tập 2
• Giải VTH Toán 7 trang 44 Tập 2