Giải Vở thực hành Toán 7 trang 46 Tập 1 Kết nối tri thức

---

Với Giải VTH Toán 7 trang 46 Tập 1 trong Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song Vở thực hành Toán lớp 7 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 trang 46.

Giải Vở thực hành Toán 7 trang 46 Tập 1 Kết nối tri thức

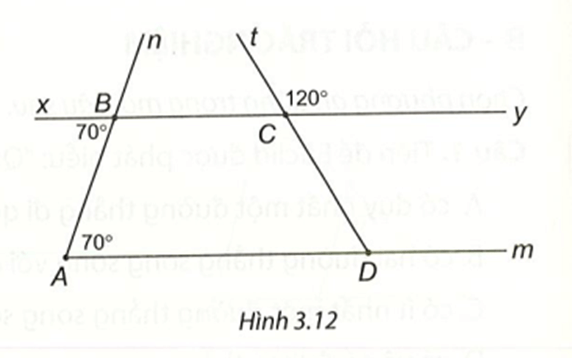
Bài 2 (3.18) trang 46 vở thực hành Toán lớp 7 Tập 1: Cho Hình 3.12.

a) Giải thích tại sao Am // By.

b) Tính $\widehat{C\text{D}m}.$

Lời giải:

a) Ta có $\widehat{ABx}=\widehat{BA\text{D}}=70°$, mà hai góc này ở vị trí so le trong

Suy ra Am // By (dấu hiệu nhận biết hai đường thẳng song song).

b) Ta có Am // By, suy ra $\widehat{tCy}=\widehat{C\text{Dm}}=120°$ (hai góc đồng vị).

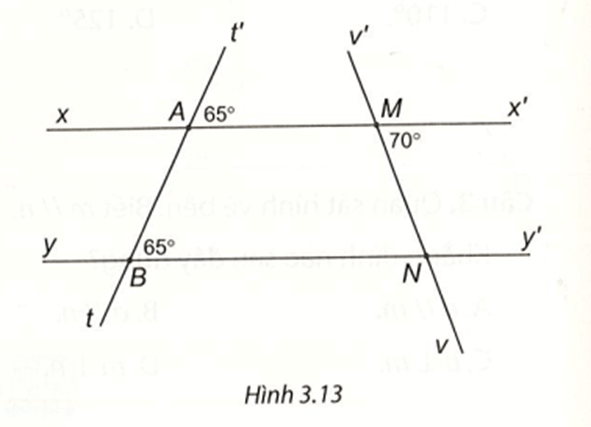
Bài 3 (3.19) trang 46 vở thực hành Toán lớp 7 Tập 1: Cho Hình 3.13

a) Giải thích tại sao xx' // yy'.

b) Tính số đo góc MNB.

Lời giải:

a) Ta có $\widehat{t^{\text{'}}AM}=\widehat{ABN}=65°.$

Mà hai góc này ở vị trí đồng vị

Suy ra xx’ // yy’ (dấu hiệu nhận biết hai đường thẳng song song).

b) Ta có xx’ // yy’ nên $\widehat{MNB}=\widehat{NM}=70°$ (2 góc so le trong).

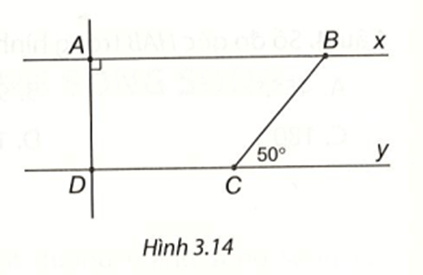
Bài 4 (3.20) trang 46 vở thực hành Toán lớp 7 Tập 1: Cho Hình 3.14, biết rằng Ax // Dy, $\hat{A}=90°,\widehat{BCy}=50°.$ Tính số đo các góc ADC và ABC.

Lời giải:

Ta có Ax // Dy, suy ra $\widehat{ABC}=\widehat{yCB}=50°$ (hai góc so le trong)

nên $\widehat{ABC}=50°.$

Ta có Ax // Dy mà AD ⊥ AB $\left(\hat{A}=90°\right)$, suy ra Dy ⊥ AD nên $\widehat{A\text{D}C}=90°.$

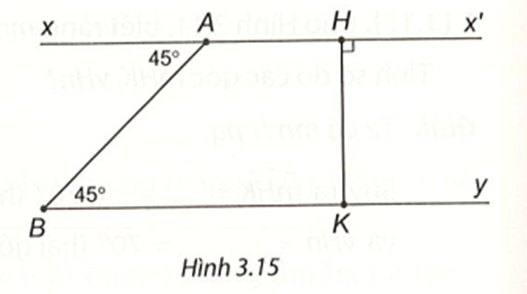
Bài 5 (3.21) trang 46 vở thực hành Toán lớp 7 Tập 1: Cho Hình 3.15. Giải thích tại sao:

a) Ax' // By;

b) By ⊥ HK.

Lời giải:

a) Ta có $\widehat{\text{BAx}}=\widehat{ABy}=45°$, mà hai góc này ở vị trí so le trong nên Ax // By hay Ax' // By (dấu hiệu nhận biết hai đường thẳng song song).

b) Ta có HK ⊥ Ax' mà Ax' // By. Suy ra By ⊥ HK.

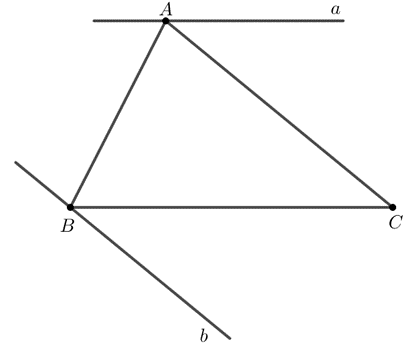
Bài 6 (3.22) trang 46 vở thực hành Toán lớp 7 Tập 1: Cho tam giác ABC. Vẽ đường thẳng a đi qua A và song song với BC. Vẽ đường thẳng b đi qua B và song song với AC. Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thẳng b? Vì sao?

Lời giải:

Theo tiên đề Euclid, chỉ vẽ được duy nhất một đường thẳng a, một đường thẳng b.

Qua điểm A nằm ngoài đoạn BC, vẽ được duy nhất một đường thẳng song song với BC. Do đó ta chỉ có thể vẽ được 1 đường thẳng a.

Qua điểm B nằm ngoài đoạn AC, vẽ được duy nhất một đường thẳng song song với AC. Do đó ta chỉ có thể vẽ được 1 đường thẳng b.

Lời giải Vở thực hành Toán lớp 7 Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song Kết nối tri thức hay khác:

• Giải VTH Toán 7 trang 45 Tập 1

• Giải VTH Toán 7 trang 47 Tập 1