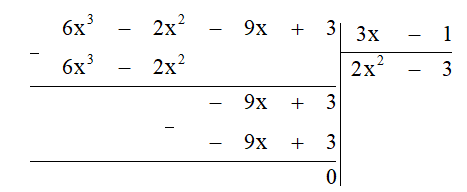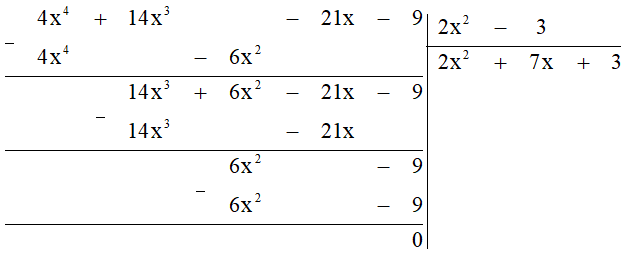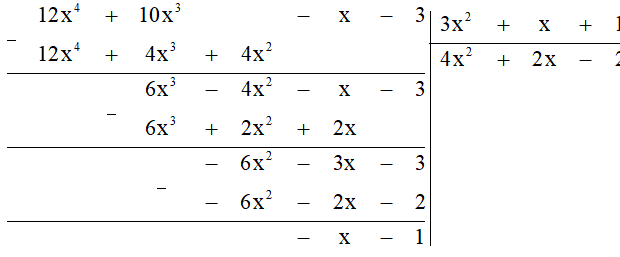Giải Vở thực hành Toán 7 trang 47 Tập 2 Kết nối tri thức

---

Với Giải VTH Toán 7 trang 47 Tập 2 trong Bài 28: Phép chia đa thức một biến Vở thực hành Toán lớp 7 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 trang 47.

Giải Vở thực hành Toán 7 trang 47 Tập 2 Kết nối tri thức

Bài 3 (7.32) trang 47 vở thực hành Toán lớp 7 Tập 2: Thực hiện các phép chia đa thức sau bằng cách đặt tính chia:

a) (6x³ - 2x² - 9x + 3) : (3x - 1);

b) (4x⁴ + 14x³ - 21x - 9) : (2x² - 3).

Lời giải:

a,

b,

Bài 4 (7.33) trang 47 vở thực hành Toán lớp 7 Tập 2: Thực hiện phép chia 0,5x⁵ + 3,2x³ - 2x² cho 0,25xⁿ trong mỗi trường hợp sau:

a) n = 2;

b) n = 3.

Lời giải:

a) Khi n = 2 ta có phép chia:

(0,5x⁵ + 3,2x³ - 2x²) : 0,25x²

= 0,5x⁵ : 0,25x² + 3,2x³ : 0,25x² - 2x² : 0,25x²

= 2x³ + 12,8x - 8

b) Khi n = 3 ta có phép chia:

(0,5x⁵ + 3,2x³ - 2x²) : 0,25x³

= 0,5x⁵ : 0,25x³ + 3,2x³ : 0,25x³ (dư – 2x²)

= 2x² + 12,8 (dư – 2x²)

Bài 5 (7.34) trang 47 vở thực hành Toán lớp 7 Tập 2: Trong mỗi trường hợp sau đây, tìm thương Q(x) và dư R(x) trong phép chia F(x) cho G(x) rồi biểu diễn F(x) dưới dạng: F(x) = G(x) . Q(x) + R(x).

a) F(x) = 6x⁴ - 3x³ + 15x² + 2x - 1; G(x) = 3x².

b) F(x) = 12x⁴ + 10x³ - x - 3; G(x) = 3x² + x + 1.

Lời giải:

a) Ta có:

(6x⁴ - 3x³ + 15x² + 2x - 1) : 3x² = 2x² – x + 5 (dư 2x – 1).

Do đó Q(x) = 2x² - x + 5; R(x) = 2x - 1.

Vậy F(x) = G(x)(2x² – x + 5) + 2x – 1.

b) Đặt tính chia:

Có nghĩa là F(x) : G(x) = 4x² + 2x – 2 (dư – x – 1).

Do đó Q(x) = 4x² + 2x - 2; R(x) = -x - 1.

Vậy F(x) = G(x)(4x² + 2x - 2) + (- x - 1).

Lời giải Vở thực hành Toán lớp 7 Bài 28: Phép chia đa thức một biến Kết nối tri thức hay khác:

• Giải VTH Toán 7 trang 46 Tập 2
• Giải VTH Toán 7 trang 48 Tập 2
• Giải VTH Toán 7 trang 49 Tập 2