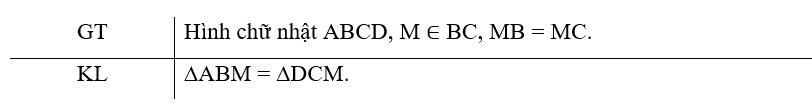Giải Vở thực hành Toán 7 trang 71 Tập 1 Kết nối tri thức
Với Giải VTH Toán 7 trang 71 Tập 1 trong Bài 15: Các trường hợp bằng nhau của tam giác vuông Vở thực hành Toán lớp 7 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 trang 71.
Giải Vở thực hành Toán 7 trang 71 Tập 1 Kết nối tri thức
Bài 3 (4.22) trang 71 vở thực hành Toán lớp 7 Tập 1: Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC. Chứng minh rằng ∆ABM = ∆DCM.
Lời giải:
Ta thấy ABM và DCM là hai tam giác lần lượt vuông tại các đỉnh B, C và ta có:
AB = CD (hai cạnh đối của hình chữ nhật bằng nhau).
MB = MC (theo giả thiết).
Vậy ∆ABM = ∆DCM (hai cạnh góc vuông).
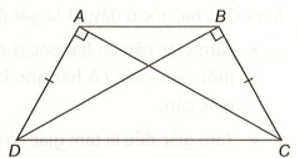
Bài 4 trang 71 vở thực hành Toán lớp 7 Tập 1: Cho hình vẽ bên. Biết , AD = BC, hãy chứng minh rằng .
Lời giải:
Ta thấy hai tam giác ADC và BCD lần lượt vuông góc tại các đỉnh A, B và có:
DC là cạnh chung
AD = BC (theo giả thiết)
Vậy ∆ADC = ∆BCD (cạnh huyền – cạnh góc vuông). Từ đây suy ra AC = BD.
Hai tam giác BAD và ABC có: AD = BC (theo giả thiết), AB là cạnh chung, BD = AC (chứng minh trên). Vậy ∆BAD = ∆ABC (c – c – c), suy ra .
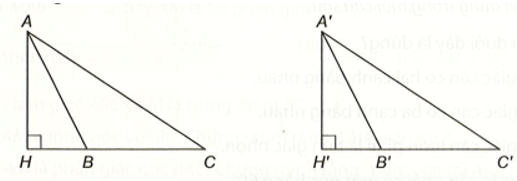
Bài 5 trang 71 vở thực hành Toán lớp 7 Tập 1: Cho hình vẽ dưới đây. Biết AB = A’B’, HB = H’B’, BC = B’C’. Chứng minh rằng AC = A’C’.
Lời giải:
Hai tam giác AHB và A’H’B’ lần lượt vuông tại H, H’ và có:
AB = A’B’, HB = H’B’ (theo giả thiết).
Vậy ∆AHB = ∆A’H’B’ (cạnh huyền – cạnh góc vuông). Do đó AH = A’H’.
Hai tam giác AHC và A’H’C’ lần lượt vuông tại H, H’ và có:
AH = A’H’ (theo chứng minh trên);
HC = HB + BC = H’B’ + B’C’ = H’C’ (theo giả thiết).
Vậy ∆AHC = ∆A’H’C’ (Hai cạnh góc vuông). Từ đó suy ra AC = A’C’.
Lời giải Vở thực hành Toán lớp 7 Bài 15: Các trường hợp bằng nhau của tam giác vuông Kết nối tri thức hay khác: