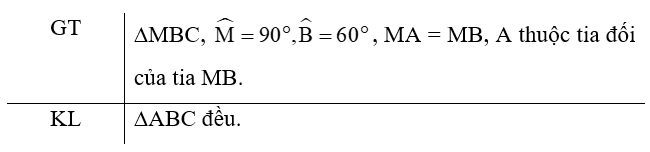Giải Vở thực hành Toán 7 trang 77 Tập 1 Kết nối tri thức

Với Giải VTH Toán 7 trang 77 Tập 1 trong Luyện tập chung trang 76, 77, 78 Vở thực hành Toán lớp 7 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 trang 77.

Giải Vở thực hành Toán 7 trang 77 Tập 1 Kết nối tri thức

Bài 4 (4.32) trang 77 vở thực hành Toán lớp 7 Tập 1: Cho tam giác MBC vuông tại M có $\hat{B}=60°.$ Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.

Lời giải:

Ta thấy hai tam giác MBC và MAC vuông tại M và có:

MB = MA (theo giả thiết);

MC là cạnh chung.

Vậy ∆MBC = ∆MAC (hai cạnh góc vuông). Do đó $\hat{A}=\hat{B}=60°$.

Suy ra $\hat{C}=180°-\hat{A}-\hat{B}=180°-60°-60°=60°$.

Vậy ABC là tam giác có ba góc bằng nhau nên đây là tam giác đều.

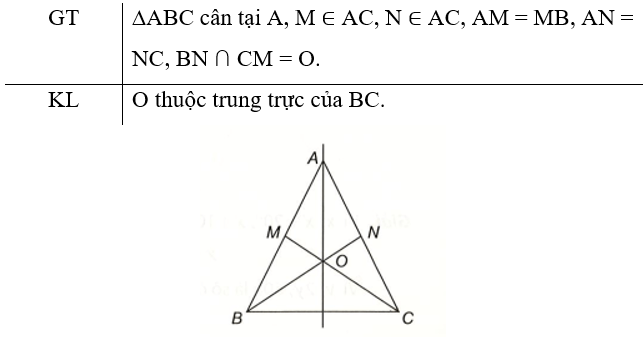
Bài 5 trang 77 vở thực hành Toán lớp 7 Tập 1: Cho tam giác ABC cân tại A. Gọi M, N lần lượt là trung điểm của AB, AC. Gọi O là giao điểm của đường thẳng BN và CM. Chứng minh rằng O nằm trên đường trung trực của đoạn thẳng BC.

Lời giải:

Hai tam giác ABN và ACM có:

AB = AC (∆ABC cân tại A);

$\widehat{BAN}=\widehat{CAM}$ (góc chung);

$AN=\frac{AC}{2}=\frac{AB}{2}=AM$ (∆ABC cân tại A).

Vậy ∆ABN = ∆ACM (c – g – c). Do đó suy ra $\widehat{ABN}=\widehat{ACM},\widehat{ANB}=\widehat{AMC}$.

Lời giải Vở thực hành Toán lớp 7 Luyện tập chung trang 76, 77, 78 Kết nối tri thức hay khác:

• Giải VTH Toán 7 trang 76 Tập 1

• Giải VTH Toán 7 trang 78 Tập 1