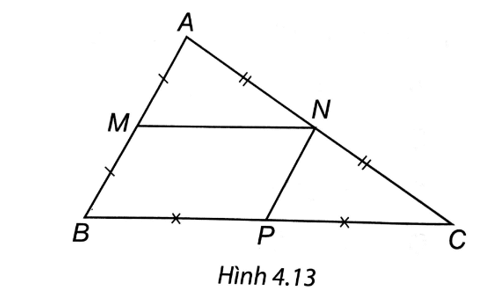
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC

Giải vở thực hành Toán 8 Bài 16: Đường trung bình của tam giác - Kết nối tri thức

Bài 2 trang 73 vở thực hành Toán 8 Tập 1: Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC.

a) Chứng minh tứ giác BMNC là hình thang.

b) Tứ giác MNPB là hình gì? Tại sao?

Lời giải:

Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC

(H.4.13). a) ∆ABC có M là trung điểm AB, N là trung điểm AC nên MN là đường trung bình của ∆ABC, suy ra MN // AC.

Xét tứ giác BMNC có MN // AC nên là tứ giác BMNC là hình thang.

b) MN là đường trung bình của ∆ABC nên $M N = \frac{1}{2} A C, M N ∥ A C .$

Xét tứ giác MNPB có: MN // BP, MN = BP nên tứ giác MNPB là hình bình hành.

Lời giải vở thực hành Toán 8 Bài 16: Đường trung bình của tam giác hay khác: