Cho hình chữ nhật ABCD có AC cắt BD tại O

Giải vở thực hành Toán 8 Bài 16: Đường trung bình của tam giác - Kết nối tri thức

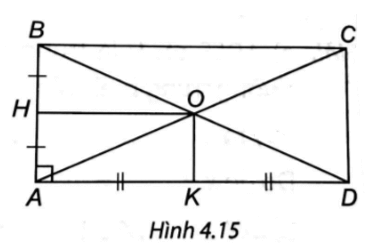
Bài 4 trang 74 vở thực hành Toán 8 Tập 1: Cho hình chữ nhật ABCD có AC cắt BD tại O. Gọi H, K lần lượt là trung điểm của AB, AD. Chứng minh tứ giác AHOK là hình chữ nhật.

Lời giải:

(H.4.15). ∆ABD có: H là trung điểm AB, O là trung điểm BD (do tứ giác ABCD là hình chữ nhật) nên HO là đường trung bình của ∆ABD.

Suy ra HO // AD và HO = $\frac{1}{2}AD.$

Xét tứ giác AHOK: HO // AK và HO = AK nên tứ giác AHOK là hình bình hành.

Ta có $\widehat{HAK}=90°$ nên tứ giác AHOK là hình chữ nhật.

Lời giải vở thực hành Toán 8 Bài 16: Đường trung bình của tam giác hay khác:

• Câu 1 trang 72 vở thực hành Toán 8 Tập 1: Mỗi tam giác có bao nhiêu đường trung bình? ...

• Câu 2 trang 72 vở thực hành Toán 8 Tập 1: Tìm độ dài x trong Hình 4.10 ...

• Câu 3 trang 73 vở thực hành Toán 8 Tập 1: Quan sát Hình 4.11 và chọn khảng định đúng ...

• Câu 4 trang 73 vở thực hành Toán 8 Tập 1: Cho tam giác ABC có chu vi bằng 20 cm. Gọi M, N, P lần lượt là trung điểm của AB, BC, AC ...

• Câu 5 trang 73 vở thực hành Toán 8 Tập 1: Cho ∆ABC đều, cạnh 3 cm; M, N là trung điểm của AB và AC. Chu vi của tứ giác MNCB bằng ...

• Bài 1 trang 73 vở thực hành Toán 8 Tập 1: Tính các độ dài x, y trong Hình 4.12 ...

• Bài 2 trang 73 vở thực hành Toán 8 Tập 1: Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC ...

• Bài 3 trang 74 vở thực hành Toán 8 Tập 1: Cho tam giác ABC, trung tuyến AM. Lấy điểm D và E trên cạnh AB sao cho AD = DE = EB ...

• Bài 5 trang 74 vở thực hành Toán 8 Tập 1: Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G ...