Cho tam giác ABC, đường cao AH. Gọi M là trung điểm của AC

Giải vở thực hành Toán 8 Bài 13: Hình chữ nhật - Kết nối tri thức

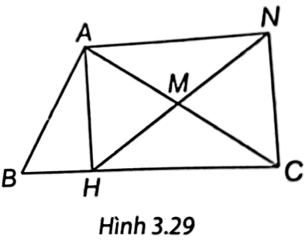
Bài 3 trang 58 vở thực hành Toán 8 Tập 1: Cho tam giác ABC, đường cao AH. Gọi M là trung điểm của AC, N là điểm sao cho M là trung điểm của HN. Chứng minh tứ giác AHCN là hình chữ nhật.

Lời giải:

(H.3.29). Ta có: AM = MC, HM = MN nên tứ giác AHCN có hai đường chéo AC, HN cắt nhau tại trung điểm mỗi đường nên AHCN là hình bình hành.

Vì $\widehat{AHC}=90°$ hay hình bình hành AHCN có một góc vuông nên AHCN là hình chữ nhật.

Lời giải vở thực hành Toán 8 Bài 13: Hình chữ nhật hay khác:

• Câu 1 trang 57 vở thực hành Toán 8 Tập 1: Hãy chọn phương án sai. A. Tứ giác có ba góc vuông là hình chữ nhật ...

• Câu 2 trang 57 vở thực hành Toán 8 Tập 1: Cho hình chữ nhật ABCD có hai đường chéo cắt nhau tại O. Chọn phương án đúng ...

• Bài 1 trang 57 vở thực hành Toán 8 Tập 1: Bằng ê ke, nêu cách kiểm tra một tứ giác có là hình chữ nhật hay không. Hãy giải thích kết quả ...

• Bài 2 trang 58 vở thực hành Toán 8 Tập 1: Bằng compa, nêu cách kiểm tra một tứ giác có là hình chữ nhật hay không ...

• Bài 4 trang 58 vở thực hành Toán 8 Tập 1: Xét một điểm M trên cạnh huyền của tam giác ABC vuông cân tại A ...

• Bài 5 trang 58 vở thực hành Toán 8 Tập 1: Cho hình chữ nhật ABCD. Gọi O là trung điểm của AC. Hạ OM vuông góc với BC tại M, ON ...