Xét một điểm M trên cạnh huyền của tam giác ABC vuông cân tại A
Giải vở thực hành Toán 8 Bài 13: Hình chữ nhật - Kết nối tri thức
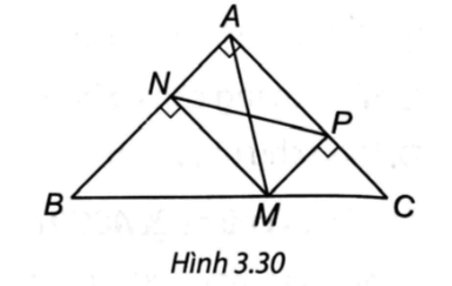
Bài 4 trang 58 vở thực hành Toán 8 Tập 1: Xét một điểm M trên cạnh huyền của tam giác ABC vuông cân tại A. Gọi N và P lần lượt là hình chiếu vuông góc của M trên các cạnh AB và AC.
a) Hỏi tứ giác MPAN là hình gì?
b) Hỏi M ở vị trí nào thì đoạn thẳng NP có độ dài ngắn nhất? Vì sao?
Lời giải:
(H.3.30). a) Tứ giác MPAN có góc vuông tại A, P, N nên là một hình chữ nhật.
b) Vì MPAN là hình chữ nhật nên NP = AM.
Với điểm M tùy ý trên BC, H là chân đường cao hạ từ A của tam giác ABC, khi đó ta có AM ≥ AH.
Vậy AM nhỏ nhất khi AM = AH, tức khi M trùng H (với H là trung điểm của BC do tam giác ABC vuông cân tại A).
Do đó NP ngắn nhất khi M là trung điểm của BC.
Lời giải vở thực hành Toán 8 Bài 13: Hình chữ nhật hay khác: