Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD
Giải vở thực hành Toán 8 Bài 12: Hình bình hành - Kết nối tri thức
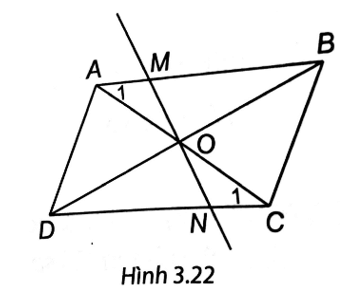
Bài 5 trang 54 vở thực hành Toán 8 Tập 1: Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Một đường thẳng đi qua O lần lượt cắt các cạnh AB, CD của hình bình hành tại hai điểm M, N. Chứng minh ∆OAM = ∆OCN. Từ đó suy ra tứ giác MBND là hình bình hành.
Lời giải:
(H.3.22). ABCD là hình bình hành nên AO = CO, BO = DO.
Xét ∆OAM và ∆OCN có: (hai góc so le trong), (hai góc đối đỉnh), AO = CO nên ∆OAM = ∆OCN (g.c.g).
Suy ra OM = ON.
Ta có OM = ON, BO = DO nên tứ giác MBND có hai đường chéo MN, BD cắt nhau tại trung điểm mỗi đường nên MBND là hình bình hành.
Lời giải vở thực hành Toán 8 Bài 12: Hình bình hành hay khác:
Câu 2 trang 52 vở thực hành Toán 8 Tập 1: Điền cụm từ thích hợp vào chỗ trống. a) Tứ giác có các ...
Câu 3 trang 52 vở thực hành Toán 8 Tập 1: Cho hình bình hành ABCD có Khi đó ...