Cho tam giác nhọn ABC có trực tâm H Vẽ các đường thẳng d vuông góc
Giải vở thực hành Toán 8 Bài 12: Hình bình hành - Kết nối tri thức
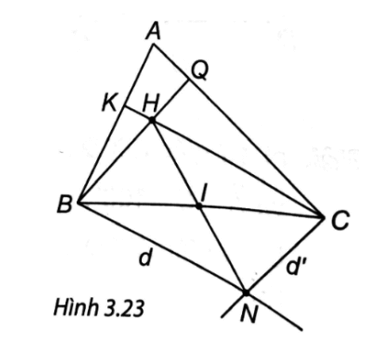
Bài 6 trang 54 vở thực hành Toán 8 Tập 1: Cho tam giác nhọn ABC có trực tâm H. Vẽ các đường thẳng d vuông góc với AB tại B, d’ vuông góc với AC tại C, d và d’ cắt nhau tại N. Chứng mình rằng:
a) Tứ giác BHCN là hình bình hành.
b) HN đi qua trung điểm I của đoạn thẳng BC.
Lời giải:
(H.3.23). Vì H là trực tâm của ∆ABC nên CH ⊥ AB, BH ⊥ AC.
Ta có CH ⊥ AB, NB ⊥ AB ⇒ CH // NB.
Tương tự BH // CN.
Từ đó, suy ra BHCN là hình bình hành.
b) Ta có BHCN là hình bình hành nên BC và HN cắt nhau tại trung điểm mỗi đường, do đó HN đi qua trung điểm I của đoạn thẳng BC.
Lời giải vở thực hành Toán 8 Bài 12: Hình bình hành hay khác:
Câu 2 trang 52 vở thực hành Toán 8 Tập 1: Điền cụm từ thích hợp vào chỗ trống. a) Tứ giác có các ...
Câu 3 trang 52 vở thực hành Toán 8 Tập 1: Cho hình bình hành ABCD có Khi đó ...