HĐ4 trang 58 Chuyên đề Toán 11
Trong HĐ2, gọi (P) là mặt phẳng hình chiếu cạnh và A là hình chiếu cạnh của A. Gọi Oz là giao tuyến của (P) và (P), Oy là giao tuyến của (P) và (P). Quay mặt phẳng (P) quanh Ox sao cho (P) trùng với (P) và quay mặt phẳng (P) quanh Oz sao cho (P) trùng với (P), khi đó ba điểm A, A, A cùng thuộc mặt phẳng (P) (H.3.14).
Giải Chuyên đề Toán 11 Bài 11: Hình chiếu vuông góc và hình chiếu trục đo - Kết nối tri thức
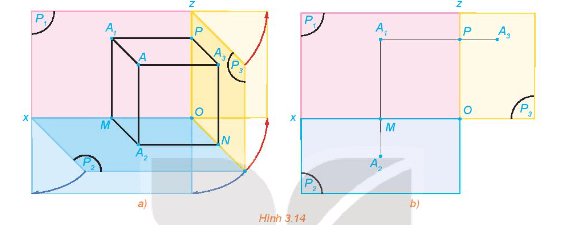
HĐ4 trang 58 Chuyên đề Toán 11: Trong HĐ2, gọi (P3) là mặt phẳng hình chiếu cạnh và A3 là hình chiếu cạnh của A. Gọi Oz là giao tuyến của (P1) và (P3), Oy là giao tuyến của (P2) và (P3). Quay mặt phẳng (P2) quanh Ox sao cho (P2) trùng với (P1) và quay mặt phẳng (P3) quanh Oz sao cho (P3) trùng với (P1), khi đó ba điểm A1, A2, A3 cùng thuộc mặt phẳng (P1) (H.3.14).
a) Đường thẳng A1A3 có vuông góc với đường thẳng Oz hay không? Khoảng cách từ A3 đến Oz có bằng khoảng cách từ A2 đến Ox hay không?
b) Trong mặt phẳng (P1), trình bày cách xác định điểm A3 khi biết hai điểm A1, A2.
Lời giải:
a) Đường thẳng A1A3 có vuông góc với đường thẳng Oz. Khoảng cách từ A3 đến Oz bằng khoảng cách từ A2 đến Ox.
b) Ta có A1A2 vuông góc với Ox nên gọi giao điểm của A1A2 với Ox là M.
Từ A1 kẻ đường thẳng song song với Ox và vuông góc với Oz. Gọi giao điểm của đường thẳng kẻ từ A1 với Oz là P.
Khoảng cách từ A3 đến Oz bằng khoảng cách từ A2 đến Ox hay A2M = A3P. Từ P kẻ A3P sao cho A1, P, A3 thẳng hàng theo thứ tự và A2M = A3P.
Lời giải Chuyên đề Toán 11 Bài 11: Hình chiếu vuông góc và hình chiếu trục đo hay, chi tiết khác: