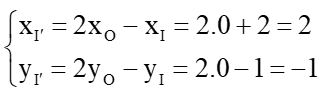Thực hành 2 trang 22 Chuyên đề Toán 11 Chân trời sáng tạo

Giải Chuyên đề Toán 11 Bài 4: Phép đối xứng tâm - Chân trời sáng tạo

Thực hành 2 trang 22 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, tìm ảnh qua Đ_O của

a) điểm M(3; –4);

b) đường thẳng d: x – 3y + 6 = 0;

c) đường tròn (C): (x + 2)² + (y – 1)² = 4.

Lời giải:

a) Gọi M’ là ảnh của M qua Đ_O.

Suy ra O là trung điểm của MM’ với M(3; –4).

Do đó 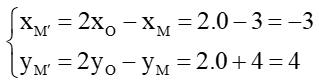Thực hành 2 trang 22 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Vậy M’(–3; 4).

b) • Chọn A(0; 2) ∈ d: x – 3y + 6 = 0.

Gọi A’là ảnh của A qua Đ_O.

Suy ra O là trung điểm của AA’ với A(0; 2)

Do đó 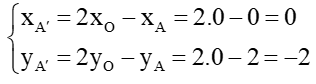Thực hành 2 trang 22 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Vì vậy A’(0; –2).

• Đường thẳng d: x – 3y + 6 = 0 có vectơ pháp tuyến $\vec{n} = (1; - 3)$ .

Gọi d’ là ảnh của d qua Đ_O.

Suy ra d’ song song hoặc trùng với d, nên d’ nhận vectơ pháp tuyến của d là $\vec{n} = (1; - 3)$ làm vectơ pháp tuyến.

Vậy đường thẳng d’ đi qua A’(0; –2) và nhận làm vectơ $\vec{n} = (1; - 3)$ pháp tuyến nên có phương trình là:

1(x – 0) – 3(y + 2) = 0 hay x – 3y – 6 = 0.

c) Đường tròn (C): (x + 2)² + (y – 1)² = 4 có tâm I(–2; 1), bán kính R = 2.

Gọi (C’) là ảnh của (C) qua Đ_O nên (C’) có tâm là ảnh của I(–2; 1) và có bán kính R’ = R = 2.

Gọi I’= Đ_O(I).

Suy ra O là trung điểm II’.

Do đó Thực hành 2 trang 22 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Vì vậy tọa độ I’(2; –1).

Vậy đường tròn (C’) là ảnh của (C) qua Đ_O, có tâm I’(2; –1) và R’ = 2 nên có phương trình là:

(x – 2)² + (y + 1)² = 4.

Lời giải Chuyên đề Toán 11 Bài 4: Phép đối xứng tâm hay, chi tiết khác: