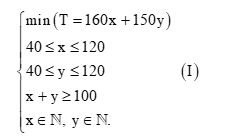Bài 1 trang 27 Chuyên đề Toán 12
Để hoàn thành hợp đồng đúng hạn, một nhà máy tổ chức cho công nhân làm việc theo hai ca, ca I từ 7h30 đến 15h30 và ca II từ 16h00 đến 22h00. Mỗi ca có số công nhân làm việc tối thiểu là 40 người và tối đa là 120 người. Số công nhân làm việc ở cả hai ca ít nhất là 100 người.
Giải Chuyên đề Toán 12 Bài 1: Vận dụng hệ bất phương trình bậc nhất để giải quyết một số bài toán quy hoạch tuyến tính - Cánh diều
Bài 1 trang 27 Chuyên đề Toán 12: Để hoàn thành hợp đồng đúng hạn, một nhà máy tổ chức cho công nhân làm việc theo hai ca, ca I từ 7h30 đến 15h30 và ca II từ 16h00 đến 22h00. Mỗi ca có số công nhân làm việc tối thiểu là 40 người và tối đa là 120 người. Số công nhân làm việc ở cả hai ca ít nhất là 100 người.
Thu nhập tăng thêm cho mỗi công nhân được tính theo Bảng 2.
Tính số lượng công nhân làm việc cho từng ca sao cho số tiền nhà máy trả cho thu nhập tăng thêm là nhỏ nhất.
Lời giải:
Gọi x và y lần lượt là số lượng công nhân làm việc cho ca I và ca II (x ∈ ℕ, y ∈ ℕ).
Số giờ làm ca I là: 15h30 – 7h30 = 8h, số giờ làm ca II là: 22h – 16h = 6h.
Thu nhập tăng thêm là: T = 20.8.x + 25.6.y = 160x + 150y (nghìn đồng).
Số công nhân làm việc ở cả hai ca là: x + y (người).
Vì số công nhân làm việc ở cả hai ca ít nhất là 100 người nên ta có thể viết dạng tổng quát của bài toán quy hoạch tuyến tính sau:
Xét hệ bất phương trình bậc nhất hai ẩn (x, y là các số thực):
Ta cần tìm giá trị nhỏ nhất của biểu thức T = 160x + 150y khi (x; y) thỏa mãn hệ bất phương trình (I’).
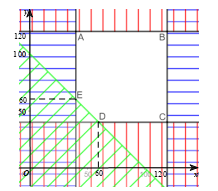
Bước 1. Xác định miền nghiệm của hệ bất phương trình (I’).
Miền nghiệm là miền ngũ giác ABCDE với tọa độ các đỉnh A(40; 120), B(120; 120), C(120; 40), D(60; 40), E(40; 60) (hình vẽ).
Bước 2. Tính giá trị của biểu thức T(x; y) = 160x + 150y tại các đỉnh của ngũ giác ABCDE:
T(40; 120) = 24 400; T(120; 120) = 37 200; T(120; 40) = 25 200;
T(60; 40) = 15 600; T(40; 60) = 15 400.
Bước 3. Ta đã biết biểu thức T = 160x + 150y đạt giá trị nhỏ nhất tại cặp số thực (x; y) là tọa độ một trong các đỉnh của ngũ giác ABCDE. So sánh năm giá trị thu được của T ở Bước 2, ta được giá trị nhỏ nhất cần tìm là T(40; 60) = 15 400.
Bước 4. Vì 40 và 60 đều là số tự nhiên nên cặp số (x; y) = (40; 60) là nghiệm của bài toán (I).
Vậy cần 40 nhân viên làm việc ca I và 60 nhân viên làm việc ca II thì số tiền nhà máy trả cho thu nhập tăng thêm là nhỏ nhất.
Lời giải bài tập Chuyên đề Toán 12 Bài 1: Vận dụng hệ bất phương trình bậc nhất để giải quyết một số bài toán quy hoạch tuyến tính hay, chi tiết khác: