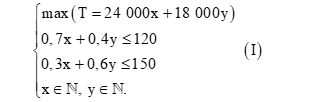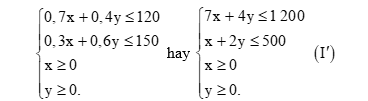Luyện tập - vận dụng 2 trang 24 Chuyên đề Toán 12
Hãy giải bài toán trong phần mở đầu.
Giải Chuyên đề Toán 12 Bài 1: Vận dụng hệ bất phương trình bậc nhất để giải quyết một số bài toán quy hoạch tuyến tính - Cánh diều
Luyện tập - vận dụng 2 trang 24 Chuyên đề Toán 12: Hãy giải bài toán trong phần mở đầu.
Lời giải:
Gọi x, y lần lượt là số lít nước sinh tố loại thứ nhất và loại thứ hai mà công ty dự định sản xuất.
Tổng số tiền công ty thu được khi bán x lít nước sinh tố loại thứ nhất và y lít nước sinh tố loại thứ hai là: T = 24 000x + 18 000y (đồng).
Số lít nước anh đào có trong x lít nước sinh tố loại thứ nhất và y lít nước sinh tố loại thứ hai là 0,7x + 0,4y (lít).
Số lít nước cam có trong x lít nước sinh tố loại thứ nhất và y lít nước sinh tố loại thứ hai là 0,3x + 0,6y (lít).
Vì lượng nguyên liệu sử dụng không vượt quá lượng dự trữ nên ta có thể viết dạng tổng quát của bài toán quy hoạch tuyến tính sau:
Xét hệ bất phương trình bậc nhất hai ẩn (x, y là các số thực):
Ta cần tìm giá trị lớn nhất của biểu thức T = 24 000x + 18 000y khi (x; y) thỏa mãn hệ bất phương trình (I’).
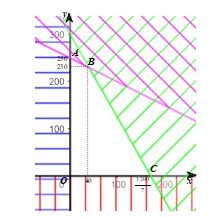
Bước 1. Xác định miền nghiệm của hệ bất phương trình (I’).
Miền nghiệm là miền tứ giác OABC với tọa độ các đỉnh O(0; 0), A(0; 250), B(40; 230); (hình vẽ).
Bước 2. Tính giá trị của biểu thức T(x; y) = 24 000x + 18 000y tại các đỉnh của tứ giác này:
T(0; 0) = 0; T(0; 250) = 4 500 000; T(40; 230) = 5 100 000;
Bước 3. Ta đã biết biểu thức T = 24 000x + 18 000y đạt giá trị lớn nhất tại cặp số thực (x; y) là tọa độ một trong các đỉnh của tứ giác OABC. So sánh bốn giá trị thu được của T ở Bước 2, ta được giá trị lớn nhất cần tìm là T(40; 230) = 5 100 000.
Bước 4. Vì 40 và 230 đều là số tự nhiên nên cặp số (x; y) = (40; 230) là nghiệm của bài toán (I).
Vậy công ty phải sản xuất 40 lít nước sinh tố loại thứ nhất và 230 lít sinh tố loại thứ hai để tổng số tiền công ty thu được là nhiều nhất.
Lời giải bài tập Chuyên đề Toán 12 Bài 1: Vận dụng hệ bất phương trình bậc nhất để giải quyết một số bài toán quy hoạch tuyến tính hay, chi tiết khác: