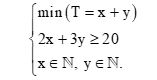Luyện tập - vận dụng 1 trang 22 Chuyên đề Toán 12
Người ta cần đóng 20 kg hàng hoá vào hai loại hộp. Mỗi chiếc hộp loại I đựng được 2 kg hàng hoá. Mỗi chiếc hộp loại II đựng được 3 kg hàng hoá. Hãy lập mô hình toán học của bài toán trên sao cho số hộp cần dùng là nhỏ nhất.
Giải Chuyên đề Toán 12 Bài 1: Vận dụng hệ bất phương trình bậc nhất để giải quyết một số bài toán quy hoạch tuyến tính - Cánh diều
Luyện tập - vận dụng 1 trang 22 Chuyên đề Toán 12: Người ta cần đóng 20 kg hàng hoá vào hai loại hộp. Mỗi chiếc hộp loại I đựng được 2 kg hàng hoá. Mỗi chiếc hộp loại II đựng được 3 kg hàng hoá. Hãy lập mô hình toán học của bài toán trên sao cho số hộp cần dùng là nhỏ nhất.
Lời giải:
Gọi x và y lần lượt là số chiếc hộp loại I và loại II cần dùng (x ∈ ℕ, y ∈ ℕ).
Tổng số hộp cần dùng là: T = x + y (hộp).
Số kg hàng hóa đựng được là: 2x + 3y (kg).
Do người ta cần đóng 20 kg hàng hóa nên ta có 2x + 3y ≥ 20.
Vậy để số hộp cần dùng là nhỏ nhất thì ta có thể mô hình bài toán như sau:
Lời giải bài tập Chuyên đề Toán 12 Bài 1: Vận dụng hệ bất phương trình bậc nhất để giải quyết một số bài toán quy hoạch tuyến tính hay, chi tiết khác: