Bài 2.6 trang 42 Chuyên đề Toán 12

Một cửa sổ có dạng phía dưới là hình chữ nhật, phía trên là nửa hình tròn có đường kính bằng chiều rộng của hình chữ nhật (H.2.17). Biết độ dài mép ngoài của cửa sổ phần sát tường (kể cả phần nửa đường tròn phía trên) là 10 m. Hãy tính các kích thước của hình chữ nhật để cửa sổ có diện tích lớn nhất (kết quả làm tròn đến chữ số thập phân thứ hai).

Giải Chuyên đề Toán 12 Bài 4: Vận dụng đạo hàm để giải quyết một số bài toán tối ưu - Kết nối tri thức

Bài 2.6 trang 42 Chuyên đề Toán 12: Một cửa sổ có dạng phía dưới là hình chữ nhật, phía trên là nửa hình tròn có đường kính bằng chiều rộng của hình chữ nhật (H.2.17). Biết độ dài mép ngoài của cửa sổ phần sát tường (kể cả phần nửa đường tròn phía trên) là 10 m. Hãy tính các kích thước của hình chữ nhật để cửa sổ có diện tích lớn nhất (kết quả làm tròn đến chữ số thập phân thứ hai).

Lời giải:

Gọi x (m) là chiều rộng của hình chữ nhật, 0 < x < 10.

Khi đó, bán kính của phần cửa sổ nửa hình tròn là $\frac{x}{2}$ (m).

Diện tích của phần cửa sổ nửa hình tròn là: $S_1=\frac{1}{2}\cdot \pi \cdot {\left(\frac{x}{2}\right)}^2=\frac{\pi x^2}{8}{\text{ (m}}^2\text{).}$

Độ dài mép ngoài của phần cửa nửa đường tròn chính là nửa chu vi đường tròn và bằng: $\pi \cdot \frac{x}{2}=\frac{\pi x}{2}\text{ (m).}$

Độ dài mép ngoài của phần cửa hình chữ nhật và cũng là chu vi hình chữ nhật, bằng: $10-\frac{\pi x}{2}\text{ (m).}$

Chiều dài của phần cửa sổ hình chữ nhật là $10-\frac{\pi x}{2}-=\frac{x}{2}=\text{10}-\frac{\left(\pi +1\right)x}{2}\text{ (m).}$

Diện tích của phần cửa sổ hình chữ nhật là:

$S_2=x\cdot \left[\text{10}-\frac{\left(\pi +1\right)x}{2}\right]=10x-\frac{\left(\pi +1\right)x^2}{2}{\text{ (m}}^2\text{).}$

Diện tích của cửa sổ là:

$S\left(x\right)=S_1+S_2=\frac{\pi x^2}{8}+10x-\frac{\left(\pi +1\right)x^2}{2}=10x-\frac{\left(3\pi +4\right)x^2}{8}{\text{ (m}}^2\text{).}$

Xét hàm $S\left(x\right)=10x-\frac{\left(3\pi +4\right)x^2}{8}$  trên khoảng (0; 10).

Ta có

$S^{\text{'}}\left(x\right)=10-\frac{\left(3\pi +4\right)x}{4},$$S^{\text{'}}\left(x\right)=0\iff 10-\frac{\left(3\pi +4\right)x}{4}=0\iff x=\frac{40}{3\pi +4}.$

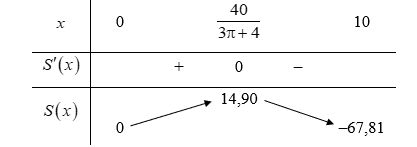
Lập bảng biến thiên của hàm số trên khoảng (0; 10):

Từ bảng biến thiên, ta có $\underset{\left(0;10\right)}{\max }S\left(x\right)\approx 14,90$  khi $x=\frac{40}{3\pi +4}\approx 2,98\text{ (m).}$

Vậy các kích thước của hình chữ nhật lần lượt là khoảng 2,98 m và $\text{10}-\frac{\left(\pi +1\right)\cdot 2,98}{2}\approx 3,83\text{ (m).}$

Lời giải bài tập Chuyên đề Toán 12 Bài 4: Vận dụng đạo hàm để giải quyết một số bài toán tối ưu hay, chi tiết khác:

• HĐ1 trang 35 Chuyên đề Toán 12: Một người đánh cá đang ở trên thuyền (vị trí A) cách bờ biển (điểm P) 2 km về phía đông trên đường bờ biển thẳng theo phương bắc nam ....

• Luyện tập 1 trang 37 Chuyên đề Toán 12: Một vật được ném từ mặt đất lên trời xiên góc α so với phương nằm ngang với vận tốc ban đầu v₀ = 9 m/s (H.2.10).....

• Luyện tập 2 trang 38 Chuyên đề Toán 12: (Định luật khúc xạ ánh sáng). Gọi v_kk là vận tốc ánh sáng trong không khí và v_n là vận tốc ánh sáng trong nước. Theo nguyên lí Fermat, một tia sáng di chuyển từ một điểm A....

• Luyện tập 3 trang 40 Chuyên đề Toán 12: Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay, doanh nghiệp đang tập trung chiến lược kinh doanh một loại xe máy với chi phí mua vào là ....

• Luyện tập 4 trang 42 Chuyên đề Toán 12: Biết rằng C(x) = 16 000 + 500x – 1,64x² + 0,004x³ là hàm chi phí và p(x) = 1 700 – 7x là hàm cầu của x đơn vị hàng hóa....

• Bài 2.7 trang 42 Chuyên đề Toán 12: Người ta muốn kéo một đường dây điện từ nhà máy điện đặt tại điểm A đến một hòn đảo nhỏ C. Biết rằng nhà máy điện nằm sát bờ biển....

• Bài 2.8 trang 43 Chuyên đề Toán 12: Một xe khách tuyến có sức chứa tối đa là 60 hành khách. Nếu chuyến xe chở x hành khách thì giá cho mỗi hành khách là ...

• Bài 2.9 trang 43 Chuyên đề Toán 12: Một công ty dự kiến chi 1 tỉ đồng sản xuất các thùng đựng sơn hình trụ với dung tích 5 ℓ. ...

• Bài 2.10 trang 43 Chuyên đề Toán 12: Giả sử C(x) = 18 000 + 500x – 1,6x² + 0,004x³ (nghìn đồng) là hàm chi phí và p(x) = 1 500 – 3x (nghìn đồng) là hàm cầu của x đơn vị một loại hàng hoá nào đó.....