Luyện tập 1 trang 37 Chuyên đề Toán 12

❮ Bài trước Bài sau ❯

Một vật được ném từ mặt đất lên trời xiên góc α so với phương nằm ngang với vận tốc ban đầu v = 9 m/s (H.2.10). Khi đó quỹ đạo chuyển động của vật tuân theo phương trình ở đó x (mét) là khoảng cách vật bay được theo phương ngang từ điểm ném, y (mét) là độ cao so với mặt đất của vật trong quá trình bay, g là gia tốc trọng trường (theo Vật lí đại cương, Nhà xuất bản Giáo dục Việt Nam, 2016).

Giải Chuyên đề Toán 12 Bài 4: Vận dụng đạo hàm để giải quyết một số bài toán tối ưu - Kết nối tri thức

Luyện tập 1 trang 37 Chuyên đề Toán 12: Một vật được ném từ mặt đất lên trời xiên góc α so với phương nằm ngang với vận tốc ban đầu v₀ = 9 m/s (H.2.10). Khi đó quỹ đạo chuyển động của vật tuân theo phương trình $y = \frac{- g}{2 v_{0}^{2} \cos^{2} α} x^{2} + x \tan α,$ ở đó x (mét) là khoảng cách vật bay được theo phương ngang từ điểm ném, y (mét) là độ cao so với mặt đất của vật trong quá trình bay, g là gia tốc trọng trường (theo Vật lí đại cương, Nhà xuất bản Giáo dục Việt Nam, 2016).

a) Tính độ cao nhất của vật trên quỹ đạo và xác định thời điểm mà vật đạt được độ cao đó (giả sử gia tốc trọng trường là g = 9,8 m/s²).

b) Xác định góc ném α để tầm ném xa của vật đạt giá trị lớn nhất.

Lời giải:

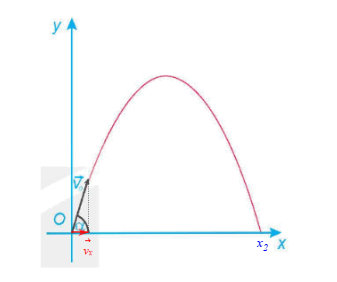
a) Ta luôn có y ≥ 0 và dễ thấy y = 0 tại x = x₁ = 0 và x = x₂ (hình vẽ).

Luyện tập 1 trang 37 Chuyên đề Toán 12

Xét $y = \frac{- g}{2 v_{0}^{2} \cos^{2} α} x^{2} + x \tan α,$ trên khoảng [0; x₂].

Đạo hàm của hàm y là $y^{'} = \frac{- g}{v_{0}^{2} \cos^{2} α} x + \tan α .$

Ta có $y^{'} = 0 \Leftrightarrow \frac{- g}{v_{0}^{2} \cos^{2} α} x + \tan α = 0$

$\Leftrightarrow x = \tan α \cdot \frac{v_{0}^{2} \cos^{2} α}{g}$

$\Leftrightarrow x = \frac{v_{0}^{2} \sin α \cdot \cos α}{g} .$

Vận dụng phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn, ta có:

$y (0) = 0; y (\frac{v_{0}^{2} \sin α \cos α}{g}) = \frac{v_{0}^{2} \sin^{2} α}{2 g}; y (x_{2}) = 0.$

Vì giá trị $y (\frac{v_{0}^{2} \sin α \cos α}{g})$ là giá trị lớn nhất trong ba giá trị trên, nên giá trị lớn nhất của y là $y = \frac{v_{0}^{2} \sin^{2} α}{2 g} (*),$ đạt được khi $x = \frac{v_{0}^{2} \sin α \cos α}{g} .$

Từ hình vẽ, ta có v_x = v₀.cosα, mà x = v_x.t nên $t = \frac{x}{v_{x}} = \frac{\frac{v_{0}^{2} \sin α \cdot \cos α}{g}}{v_{0} \cdot c o s α} = \frac{v_{0} \sin α}{g} . (* *)$

Thay v₀ = 9 m/s và g = 9,8 m/s² vào (*) và (**) ta được:

$y = \frac{9^{2} \cdot \sin^{2} α}{2 \cdot 9, 8} = \frac{405 \sin^{2} α}{98},$ tại $t = \frac{9 \sin α}{9, 8} = \frac{45 \sin α}{49} .$

Vậy vật đạt độ cao nhất trên quỹ đạo là $\frac{405 \sin^{2} α}{98} (m)$ tại thời điểm $\frac{45 \sin α}{49}$ (s).

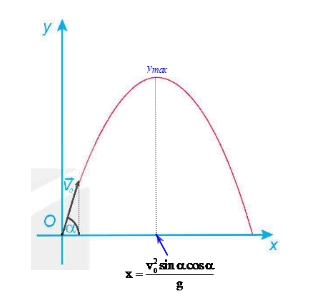
b) Từ câu a, ta có hình vẽ như sau:

Luyện tập 1 trang 37 Chuyên đề Toán 12

Khi đó, tầm ném xa của vật là:

$L = \frac{2 v_{0}^{2} \sin α \cos α}{g} = \frac{v_{0}^{2} \sin 2 α}{g} .$ $x = \frac{v_{0}^{2} \sin α \cos α}{g}$

Xét hàm số $L = \frac{v_{0}^{2} \sin 2 α}{g}$ trên đoạn [0°; 90°].

Đạo hàm của hàm L là $L^{'} = \frac{2 v_{0}^{2} \cos 2 α}{g} .$

Ta có $L^{'} = 0 \Leftrightarrow \frac{2 v_{0}^{2} \cos 2 α}{g} = 0 \Leftrightarrow \cos 2 α = 0 \Leftrightarrow 2 α = 90 ° \Leftrightarrow α = 45 ° .$

Vận dụng phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn, ta có:

$L (0) = 0; L (45 °) = \frac{v_{0}^{2}}{g}; L (90 °) = 0.$

Vì giá trị L(45°) là giá trị lớn nhất trong ba giá trị trên, nên giá trị nhỏ nhất của L đạt được khi α = 45°.

Vậy để tầm ném xa của vật đạt giá trị lớn nhất thì góc ném là 45°.

Lời giải bài tập Chuyên đề Toán 12 Bài 4: Vận dụng đạo hàm để giải quyết một số bài toán tối ưu hay, chi tiết khác:

Xem thêm lời giải bài tập Chuyên đề học tập Toán 12 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯