Bài 2.9 trang 43 Chuyên đề Toán 12

Một công ty dự kiến chi 1 tỉ đồng sản xuất các thùng đựng sơn hình trụ với dung tích 5 ℓ. Giá sản xuất mặt xung quanh là 100 nghìn đồng m, giá sản xuất mặt đáy là 120 nghìn đồng/m. Hỏi công ty có thể sản xuất được tối đa bao nhiêu thùng sơn? (Giả sử chi phí cho các mối nối không đáng kể)

Giải Chuyên đề Toán 12 Bài 4: Vận dụng đạo hàm để giải quyết một số bài toán tối ưu - Kết nối tri thức

Bài 2.9 trang 43 Chuyên đề Toán 12: Một công ty dự kiến chi 1 tỉ đồng sản xuất các thùng đựng sơn hình trụ với dung tích 5 ℓ. Giá sản xuất mặt xung quanh là 100 nghìn đồng m², giá sản xuất mặt đáy là 120 nghìn đồng/m². Hỏi công ty có thể sản xuất được tối đa bao nhiêu thùng sơn? (Giả sử chi phí cho các mối nối không đáng kể)

Lời giải:

Đổi 5 ℓ = 5 dm³ = 0,005 m³.

Gọi x (m) là bán kính của đáy thùng đựng sơn hình trụ, x > 0.

Khi đó, chiều cao của thùng đựng sơn hình trụ là: $\frac{0,005}{\pi x^2}\text{ (m).}$

Diện tích xung quanh của thùng đựng sơn hình trụ là: $S_{xq}=2\pi x\cdot \frac{0,005}{\pi x^2}=\frac{\text{0,01}}{x}{\text{ (m}}^2\text{).}$

Diện tích đáy của thùng đựng sơn hình trụ là: S_đáy = πx² (m²).

Giá sản xuất mặt xung quanh của một thùng đựng sơn là: $100\cdot \frac{\text{0,01}}{x}=\frac{1}{x}$ (nghìn đồng).

Giá sản xuất hai mặt đáy của một thùng đựng sơn là: 120.2πx² = 240πx² (nghìn đồng).

Chi phí sản xuất một thùng sơn là: $C\left(x\right)=\frac{1}{x}+240\pi x^2$ (nghìn đồng) với x > 0.

Ta có $C^{\text{'}}\left(x\right)=-\frac{1}{x^2}+480\pi x.$

$C^{\text{'}}\left(x\right)=0\iff -\frac{1}{x^2}+480\pi x=0\iff 480\pi x^3=1\iff x=\sqrt[3]{\frac{1}{480\pi }}.$

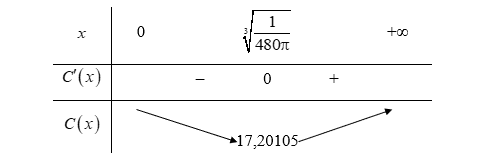
Lập bảng biến thiên của hàm số trên khoảng (0; +∞).

Từ bảng biến thiên, ta có $\underset{\left(0;+\infty \right)}{\min }C\left(x\right)\approx 17,20105$  khi $x=\sqrt[3]{\frac{1}{480\pi }}\approx 0,0872.$

Khi đó, chi phí thấp nhất để sản xuất một thùng sơn là khoảng 17,20105 nghìn đồng hay 17 201,05 đồng.

Ta có: 1 000 000 : 17 210,05 ≈ 58 135,98.

Vậy công ty có thể sản xuất được tối đa 58 135 thùng sơn.

Lời giải bài tập Chuyên đề Toán 12 Bài 4: Vận dụng đạo hàm để giải quyết một số bài toán tối ưu hay, chi tiết khác:

• HĐ1 trang 35 Chuyên đề Toán 12: Một người đánh cá đang ở trên thuyền (vị trí A) cách bờ biển (điểm P) 2 km về phía đông trên đường bờ biển thẳng theo phương bắc nam ....

• Luyện tập 1 trang 37 Chuyên đề Toán 12: Một vật được ném từ mặt đất lên trời xiên góc α so với phương nằm ngang với vận tốc ban đầu v₀ = 9 m/s (H.2.10).....

• Luyện tập 2 trang 38 Chuyên đề Toán 12: (Định luật khúc xạ ánh sáng). Gọi v_kk là vận tốc ánh sáng trong không khí và v_n là vận tốc ánh sáng trong nước. Theo nguyên lí Fermat, một tia sáng di chuyển từ một điểm A....

• Luyện tập 3 trang 40 Chuyên đề Toán 12: Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay, doanh nghiệp đang tập trung chiến lược kinh doanh một loại xe máy với chi phí mua vào là ....

• Luyện tập 4 trang 42 Chuyên đề Toán 12: Biết rằng C(x) = 16 000 + 500x – 1,64x² + 0,004x³ là hàm chi phí và p(x) = 1 700 – 7x là hàm cầu của x đơn vị hàng hóa....

• Bài 2.6 trang 42 Chuyên đề Toán 12: Một cửa sổ có dạng phía dưới là hình chữ nhật, phía trên là nửa hình tròn có đường kính bằng chiều rộng của hình chữ nhật (H.2.17). ...

• Bài 2.7 trang 42 Chuyên đề Toán 12: Người ta muốn kéo một đường dây điện từ nhà máy điện đặt tại điểm A đến một hòn đảo nhỏ C. Biết rằng nhà máy điện nằm sát bờ biển....

• Bài 2.8 trang 43 Chuyên đề Toán 12: Một xe khách tuyến có sức chứa tối đa là 60 hành khách. Nếu chuyến xe chở x hành khách thì giá cho mỗi hành khách là ...

• Bài 2.10 trang 43 Chuyên đề Toán 12: Giả sử C(x) = 18 000 + 500x – 1,6x² + 0,004x³ (nghìn đồng) là hàm chi phí và p(x) = 1 500 – 3x (nghìn đồng) là hàm cầu của x đơn vị một loại hàng hoá nào đó.....