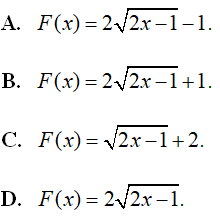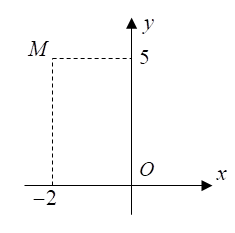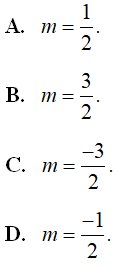Top 30 Đề thi Toán 12 Học kì 2 năm 2024 (có đáp án)
Trọn bộ 30 đề thi Toán 12 Học kì 2 sách mới Kết nối tri thức, Chân trời sáng tạo, Cánh diều có đáp án và ma trận sẽ giúp bạn ôn tập và đạt điểm cao trong bài thi Toán 12.
Top 30 Đề thi Toán 12 Học kì 2 năm 2024 (có đáp án)
Xem thử Đề thi CK2 Toán 12 KNTT Xem thử Đề thi CK2 Toán 12 CTST Xem thử Đề thi CK2 Toán 12 CD
Chỉ từ 150k mua trọn bộ đề thi Toán 12 Học kì 2 bản word có lời giải chi tiết, dễ dàng chỉnh sửa:
- B1: gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án
Xem thử Đề thi CK2 Toán 12 KNTT Xem thử Đề thi CK2 Toán 12 CTST Xem thử Đề thi CK2 Toán 12 CD
Sở Giáo dục và Đào tạo ...
Đề thi Học kì 2 - Kết nối tri thức
Năm học 2024 - 2025
Môn: Toán 12
Thời gian làm bài: phút
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Mệnh đề nào dưới đây đúng?
A. .
B. .
C. .
D. .
Câu 2. Cho ; . Tích phân bằng
A. .
B. .
C. .
D. .
Câu 3. Họ nguyên hàm của hàm số là
A. .
B. .
C. .
D. .
Câu 4. Tích phân bằng
A. ln 2 - 1.
B. ln 2 + 3.
C. ln 2 + 1.
D. ln 2 + 2.
Câu 5. Nếu các số hữu tỉ a, b thỏa mãn thì giá trị của biểu thức a + b bằng
A. 4.
B. 6.
C. 5.
D. 3.
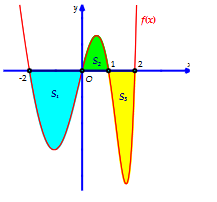
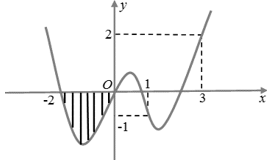
Câu 6. Cho hàm số y = f(x) liên tục trên đoạn [-2; 2], có đồ thị tạo với trục hoành một hình phẳng gồm 3 phần có diện tích S1; S2; S3 như hình vẽ bên dưới
Tích phân bằng
A. S2 + S3 - S1.
B. S1 - S2 + S3.
C. S1 + S2 + S3.
D. -S1 + S2 - S3.
Câu 7. Trong không gian Oxyz cho mặt phẳng (P): 2x - y + z -3 = 0. Véctơ nào dưới đây là một véctơ pháp tuyến của mặt phẳng (P)?
A. (2;1;1).
B. (3;-1;-1).
C. (-2;1;-1).
D. (-2;1;1).
Câu 8. Trong không gian Oxyz, cho đường thẳng . Phương trình tham số của đường thẳng d là
A. .
B. .
C. .
D. .
Câu 9. Trong không gian Oxyz, mặt phẳng đi qua điểm M(1;1;-1) và vuông góc với đường thẳng có phương trình là
A. 2x + 2y + z + 3 = 0.
B. x - 2y - z = 0.
C. 2x + 2y + z -3 = 0.
D. x - 2y - z - 2 = 0.
Câu 10. Trong không gian Oxyz cho hai đường thẳng , . Tìm tất cả giá trị thực của m để d1 vuông góc với d2.
A. m = -1.
B. m = 1.
C. m = -5.
D. m = 5.
Câu 11. Cho hai biến cố A và B với P(A) = 0,3; P(B) = 0,5; P(B|A) = 0,9. Khi đó xác suất của biến cố A ∩ B là
A. .
B. .
C. .
D. .
Câu 12. Cho hai biến cố A, B thoả mãn P(A) = 0,4; P(B) = 0,3; P(A|B) = 0,25. Khi đó, P(B|A) bằng
A. 0,1875.
B. 0,48.
C. 0,333.
D. 0,95.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
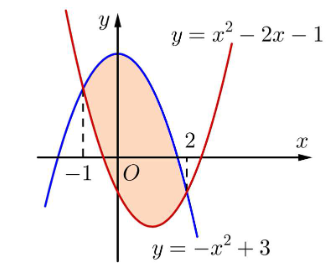
Câu 1. Cho hình phẳng (H) là phần tô đậm trong hình sau. Khi đó:
a) Hình phẳng (H) giới hạn bởi đồ thị các hàm số y = x2 - 2x -1, y = x2 + 3 và hai đường thẳng x = -1; x = 2.
b) Diện tích hình phẳng (H) là .
c) Diện tích hình phẳng (H) là .
d) Nếu (với a, b là các số nguyên tố) thì a2 + b2 = 29.
Câu 2. Trong không gian Oxyz, cho đường thẳng và mặt phẳng (P): x + y - 5 = 0.
a) Vectơ là một vectơ chỉ phương của ∆.
b) Góc giữa hai mặt phẳng (P) và (Oyz) bằng 45°.
c) Đường thẳng đi qua N(2;3;-4) và song song với ∆ có phương trình là .
d) Đường thẳng d vuông góc ∆ và tạo với (P) một góc 45° có một vectơ chỉ phương là .
Câu 3. Trong không gian Oxyz cho mặt cầu (S) có phương trình .
a) Đường kính mặt cầu bằng 8.
b) Mặt cầu (S) đi qua điểm A(-1;3;0).
c) Khoảng cách từ tâm mặt cầu đến mặt phẳng (Oyz) bằng 2.
d) Mặt phẳng (P) có phương trình x + 2y - 2z - 2 = 0 tiếp xúc với mặt cầu (S).
Câu 4. Bạn Nam tham gia một gian hàng trò chơi dân gian trong hội xuân của trường. Trò chơi có hai lượt chơi. Xác suất để Nam thắng ở lượt chơi thứ nhất là 0,6. Nếu Nam thắng ở lượt chơi thứ nhất thì xác suất Nam thắng ở lượt chơi thứ hai là 0,8. Ngược lại, nếu Nam thua ở lượt chơi thứ nhất thì xác suất Nam thắng ở lượt chơi thứ hai là 0,3. Xét các biến cố:
A: “Nam thắng ở lượt chơi thứ nhất”.
B: “Nam thắng ở lượt chơi thứ hai”.
a) P(A) = 0,8.
b) P(B|A) = 0,6.
c) .
d) Xác suất Nam thắng ở lượt chơi thứ nhất khi đã thắng ở lượt chơi thứ hai là khoảng 80%.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời câu 1 đến câu 6.
Câu 1. Cho hàm số . Biết F(x) là một nguyên hàm của f(x) thỏa mãn F(1) = 3. Khi đó F(5) = a + ln b với a,b ∈ ℕ. Tính tích T = ab.
Câu 2. Biết giá trị tích phân có dạng với a,b ∈ ℤ. Tính S = a2 + b2.
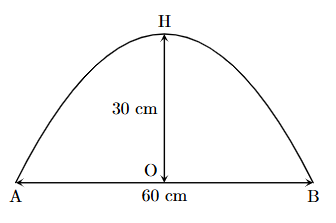
Câu 3. Bạn An cần mua một chiếc gương có viền là đường parabol bậc 2 (xem hình vẽ). Biết rằng đoạn AB = 60 cm, OH = 30 cm. Diện tích của chiếc gương bạn An mua bằng bao nhiêu cm2?
Câu 4. Khi gắn hệ tọa độ Oxyz (đơn vị trên mỗi trục tính theo kilômét) vào một trận địa pháo phòng không, mặt phẳng (Oxy) trùng với mặt đất. Trong tập luyện, một vùng mặt phẳng trong tầm hoạt động của pháo được giữ bởi 3 điểm pháo A(3;0;0); B(0;1;5;0); C(0;0;-1;5). Một mục tiêu bay từ điểm M(5;2;4) tới N(1;0;-2). Khoảng cách từ điểm pháo A tới vị trí va chạm của mục tiêu khi tới mặt phẳng là bao nhiêu? (làm tròn kết quả đến hàng phần trăm).
Câu 5. Trong không gian với hệ tọa độ Oxyz, đài kiểm soát không lưu sân bay có tọa độ O(0;0;0), mỗi đơn vị trên trục ứng với 1 km. Máy bay bay trong phạm vi cách đài kiểm soát 417 km sẽ hiển thị trên màn hình ra đa. Một máy bay đang ở vị trí A(-688;-185;8), chuyển động theo đường thẳng d có vectơ chỉ phương là và hướng về đài kiểm soát không lưu. Tọa độ của vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa là M(a;b;c). Khi đó a + b + c bằng bao nhiêu?
Câu 6. Một doanh nghiệp có 45% nhân viên là nữ. Tỉ lệ nhân viên nữ và tỉ lệ nhân viên nam mua bảo hiểm nhân thọ lần lượt là 7% và 5%. Gặp ngẫu nhiên một nhân viên của doanh nghiệp. Biết rằng nhân viên đó có mua bảo hiểm nhân thọ. Xác suất nhiên viên đó là nam bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Sở Giáo dục và Đào tạo ...
Đề thi Học kì 2 - Chân trời sáng tạo
Năm học 2024 - 2025
Môn: Toán 12
Thời gian làm bài: phút
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Nếu f(1) = 2 và thì f(3) bằng
A. 8.
B. -4.
C. 4.
D. 3.
Câu 2. Gọi S là diện tích hình phẳng giới hạn bởi các đường y = ln x, y = 0, x = 1, x = e. Mệnh đề nào dưới đây đúng?
A. .
B. .
C. .
D. .
Câu 3. Trong không gian Oxyz mặt phẳng (α): -2x + 3y - z + 5 = 0 đi qua điểm nào dưới đây?
A. N(5;1;-2).
B. Q(2;1;-1).
C. M(2;2;-3).
D. P(-3;2;4).
Câu 4. Trong không gian Oxyz đường thẳng có một vectơ chỉ phương là
A. .
B. .
C. .
D. .
Câu 5. Trong không gian Oxyz, phương trình nào dưới đây là phương trình của mặt cầu tâm I(1;0;-2) bán kính R = 4?
A. .
B. .
C. .
D. .
Câu 6. Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(2;2;1) và có một vectơ pháp tuyến . Phương trình mặt phẳng (P) là:
A. 5x + 2y - 3z - 17 = 0.
B. 2x + 2y + z - 11 = 0.
C. 5x + 2y - 3z - 11 = 0.
D. 2x + 2y + z - 17 = 0.
Câu 7. Trong không gian Oxyz, cho hai điểm M(3;-2;1), N(1;2;3). Phương trình đường thẳng MN là
A. .
B. .
C. .
D. .
Câu 8. Trong không gian với hệ trục tọa độ Oxyz. Tính góc giữa mặt phẳng (Oxy) và mặt phẳng (P) có phương trình (P): x + z + 1 = 0.
A. 20°.
B. 45°.
C. 60°.
D. 90°.
Câu 9. Trong không gian Oxyz cho hai điểm A(1;-2;-3), B(-1;4;1) và đường thẳng . Phương trình đường thẳng ∆ đi qua trung điểm của đoạn AB và song song với đường thẳng d là
A. .
B. .
C. .
D. .
Câu 10. Trong không gian Oxyz, cho điểm I(1;0;2) và mặt phẳng (P): x - 2y + 2z + 4 = 0. Mặt cầu (S) tâm I tiếp xúc với mặt phẳng (P) có phương trình là
A. .
B. .
C. .
D. .
Câu 11. Cho hai biến cố A và B , với P(A) = 0,6, P(B) = 0,7, P(A ∩ B) = 0,3. Tính P(A|B).
A. .
B. .
C. .
D. .
Câu 12. Trong một đợt kiểm tra sức khoẻ, có một loại bệnh X mà tỉ lệ người mắc bệnh là 0,2% và một loại xét nghiệm Y mà ai mắc bệnh X khi xét nghiệm Y cũng có phản ứng dương tính. Tuy nhiên, có 6% những người không bị bệnh X lại có phản ứng dương tính với xét nghiệm Y. Chọn ngẫu nhiên 1 người trong đợt kiểm tra sức khoẻ đó. Giả sử người đó có phản ứng dương tính với xét nghiệm Y. Xác suất người đó bị mắc bệnh X là bao nhiêu (làm tròn kết quả đến hàng phần trăm)?
A. 0,3.
B. 0,03.
C. 0,04.
D. 0,4.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Một vật chuyển động với gia tốc a(t) = 2cost (m/s2).
a) Tại thời điểm bắt đầu chuyển động, vật có vận tốc bằng 0. Khi đó, vận tốc của vật được biểu diễn bởi hàm số v(t) = 2sint (m/s).
b) Vận tốc của vật tại thời điểm là 1 m/s.
c) Quãng đường vật đi được từ thời điểm t = 0(s) (s) đến thời điểm t = π (s) là 4 m.
d) Quãng đường vật đi được từ thời điểm (s) đến thời điểm là 2 m.
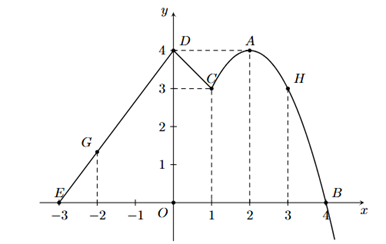
Câu 2. Đồ thị của hàm số y = f(x) liên tục trên đoạn [-3;5] như hình vẽ dưới đây (phần cong của đồ thị là một phần của Parabol y = ax2 + bx + c).
a) Diện tích tam giác ODE bằng 6.
b) Diện tích hình phẳng giới hạn bởi Parabol và đường thẳng CB bằng .
c) Giá trị của bằng .
d) Gọi diện tích tam giác OED là S1 và diện tích hình phẳng giới hạn bởi phần cong Parabol, trục Ox và đường thẳng x = 1 là S2. Khi đó 3S1 > 2S2.
Câu 3. Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng và mặt phẳng (P): 3x + y - z - 5 = 0. Mặt cầu (S) có tâm I thuộc đường thẳng d và cắt mặt phẳng (P) theo giao tuyến là đường tròn lớn nhất có bán kính r = 5.
a) Mặt phẳng (P): 3x + y - z - 5 = 0 có vectơ pháp tuyến .
b) Tọa độ tổng quát của tâm I là (t;-1 + 2t;-2-t).
c) d(I,(P)) = 3.
d) Mặt cầu (S) có phương trình là .
Câu 4. Một lớp học có 50 học sinh, trong đó có 20 học sinh nam và 30 học sinh nữ. Khi tổng kết cuối năm, lớp có 20 học sinh giỏi, trong đó có 8 học sinh nam và 12 học sinh nữ. Chọn ngẫu nhiên 1 học sinh trong lớp.
a) Xác suất học sinh được chọn là học sinh giỏi bằng 0,4.
b) Xác suất học sinh được chọn là học sinh nữ bằng 0,5.
c) Xác suất học sinh được chọn vừa là học sinh giỏi và là học sinh nữ bằng 0,6.
d) Biết rằng học sinh được chọn là nữ, xác suất học sinh đó là học sinh giỏi bằng 0,4.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời câu 1 đến câu 6.
Câu 1. Cho hàm số bậc hai f(x) = ax2 + bx + x (a ≠ 0) có đồ thị là một parabol (P) có đỉnh S(1;-2) và cắt trục tung tại điểm có tung độ bằng 1. Biết hàm số F(x) là một nguyên hàm của f(x) và đồ thị y = F(x) cũng cắt trục tung tại điểm có tung độ bằng 1. Khi đó đồ thị hàm số y = F(x) đi qua điểm M(12;m). Giá trị của m bằng bao nhiêu?
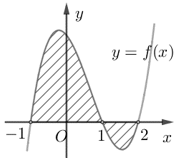
Câu 2. Cho hàm số f(x) liên tục trên ℝ và . Tính .
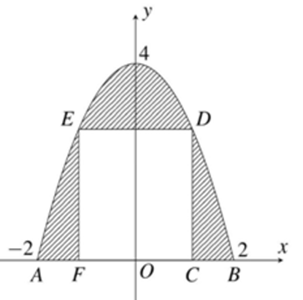
Câu 3. Một chiếc cổng có hình dạng là một parabol (P) có kích thước như hình vẽ, biết chiều cao cổng bằng 4 m, AB = 4 m. Người ta thiết kế cửa đi là một hình chữ nhật CDEF (với C, F ∈ AB; D, E ∈ (P)), phần còn lại (phân tô đậm) dùng để trang trí. Biết chi phí để trang trí phần tô đậm là 1 000 000 đồng/m2. Gắn hệ trục tọa độ Oxy như hình bên.
Chi phí trang trí tối thiểu là bao nhiêu triệu đồng? (kết quả làm tròn đến hàng phần mười).
Câu 4. Trong không gian với hệ tọa độ Oxyz, một cabin cáp treo xuất phát từ điểm A(10;3;0) và chuyển động đều theo đường cáp có vectơ chỉ phương là với tốc độ 4,5 m/s (đơn vị trên mỗi trục tọa độ là mét).
Giả sử cabin dừng ở điểm B có hoành độ xB = 550. Khi đó quãng đường AB dài bao nhiêu mét?
Câu 5. Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa đô là km), một máy bay đang ở vị trí A(3;2;1) và sẽ hạ cánh ở vị trí B(2;-5;0) trên đường băng. Có một đám mây được mô phỏng bởi mặt phẳng (P) tiếp xúc với mặt cầu (S): tại . Tính độ cao của máy bay khi đi xuyên qua đám mây để hạ cánh (giả sử mặt đất ở vị trí máy bay đang bay được coi là mặt phẳng (Oxy)).
Câu 6. Chuồng I có 5 con gà mái, 2 con gà trống. Chuồng II có 3 con gà mái, 5 con gà trống. Bác Mai bắt một con gà trong số đó theo cách sau: Bác tung một con xúc xắc cân đối, đồng chất. Nếu số chấm chia hết cho 3 thì bác chọn chuồng I, nếu số chấm không chia hết cho 3 thì bác chọn chuồng II. Sau đó, từ chuồng đã chọn bác bắt ngẫu nhiên một con gà. Gọi P là xác suất để bác Mai bắt được con gà mái. Khi đó 84P bằng bao nhiêu?
Sở Giáo dục và Đào tạo ...
Đề thi Học kì 2 - Cánh diều
Năm học 2024 - 2025
Môn: Toán 12
Thời gian làm bài: phút
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Mệnh đề nào dưới đây sai?
A. .
B. .
C. .
D. .
Câu 2. Cho , . Khi đó bằng
A. -1.
B. 1.
C. -3.
D. 3.
Câu 3. Họ các nguyên hàm của hàm số là:
A. .
B. .
C. .
D. .
Câu 4. Cho hàm số f(x) có và . Khi đó bằng
A. .
B. 2π.
C. .
D. .
Câu 5. Diện tích của hình phẳng giới hạn bởi các đường y = cos2x; y = 0; x = 0; bằng
A. .
B. .
C. .
D. .
Câu 6. Cho hình phẳng (H) giới hạn bởi các đường , y = 0, x = 0, x = 2. Quay hình phẳng (H) quanh trục hoành tạo nên một khối tròn xoay có thể tích bằng
A. .
B. .
C. .
D. .
Câu 7. Trong không gian Oxyz, mặt cầu (S): có bán kính bằng
A. .
B. 25.
C. 5.
D. 75.
Câu 8. Trong không gian Oxyz, cho 3 điểm A(1;-2;0) B(2;-1;3) C(0;-1;1) đường trung tuyến AM của tam giác ABC có phương trình là
A. .
B. .
C. .
D. .
Câu 9. Cho hai mặt phẳng và . Tính góc giữa hai mặt phẳng (P1) và (P2).
A. 70°.
B. 45°.
C. 30°.
D. 60°.
Câu 10. Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt cầu có tâm I(-3;1;2), bán kính R = 3 là
A. .
B. .
C. .
D. .
Câu 11. Cho hai biến cố A, B có xác suất P(A) = 0,4; P(B) = 0,6; P(AB) = 0,2. Tính xác suất P(A|B).
A. .
B. .
C. 0,3.
D. 0,25.
Câu 12. Cho . Giá trị của P(B) là
A. .
B. .
C. .
D. .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Một ô tô đang chạy với vận tốc 20 m/s thì người ta nhìn thấy chướng ngại vật nên đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc v(t) = -2t + 20, trong đó t là thời gian (tính bằng giây) kể từ lúc đạp phanh.
a) Ô tô dừng lại sau 10 giây.
b) Quãng đường s(t) mà xe ô tô đi được trong thời gian t giây là một nguyên hàm của hàm số v(t).
c) Từ thời điểm đạp phanh đến khi dừng lại, ô tô đi được quãng đường là 90 m.
d) Quãng đường mà ô tô đi được trong 15 giây cuối bằng 125 m.
Câu 2. Trong không gian Oxyz, cho đường thẳng và điểm A(3;2;0).
a) Đường thẳng (d) đi qua điểm A(3;2;0).
b) Đường thẳng (d) có một vectơ chỉ phương là .
c) H(1;1;2) là hình chiếu của A lên đường thẳng d.
d) A'(-1;0;4) là điểm đối xứng với A qua đường thẳng d.
Câu 3. Trong không gian Oxyz, cho điểm A(2;1;0) và mặt phẳng (P): 2x + y - 2z + 1 = 0.
a) Một vectơ pháp tuyến của mặt phẳng (P) là .
b) Điểm A thuộc mặt phẳng (P).
c) Khoảng cách từ điểm A đến mặt phẳng (P) bằng 3.
d) Phương trình mặt cầu tâm A và tiếp xúc với mặt phẳng (P) là .
Câu 4. Trong một hộp có 20 viên bi xanh và 4 viên bi đỏ, các viên bi đều có hình dạng và kích thước giống nhau. Một học sinh lấy ngẫu nhiên lần lượt 2 viên bi (lấy không hoàn lại) trong hộp.
a) Xác suất để lần thứ nhất lấy được viên bi đỏ là .
b) Xác suất để lần thứ hai lấy được viên bi đỏ, biết lần thứ nhất lấy được viên bi đỏ là .
c) Xác suất để cả hai lần đều lấy được viên bi đỏ là .
d) Xác suất để ít nhất một lần lấy được viên bi xanh là .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời câu 1 đến câu 6.
Câu 1. Cho với m,n,a,b, là các hằng số thực và a < 0 < b. Giá trị của biểu thức m + n bằng bao nhiêu?
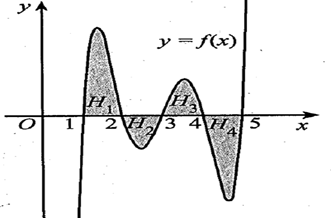
Câu 2. Gọi H1; H2: H3; H4 là các hình phẳng giới hạn bởi đồ thị hàm số liên tục y = f(x) và trục hoành với x lần lượt thuộc các đoạn [1;2], [2;3], [3;4], [4;5] (tham khảo hình vẽ). Biết rằng các hình H1; H2: H3; H4 lần lượt có diện tích bằng . Giá trị bằng bao nhiêu?
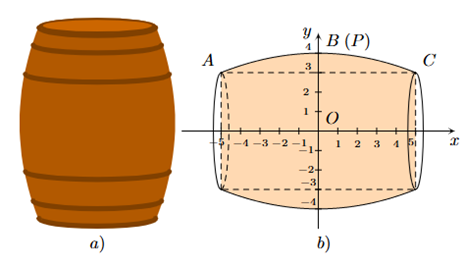
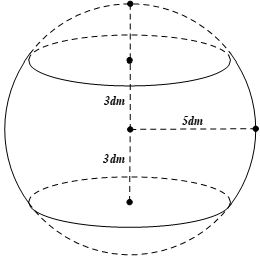
Câu 3. Một thùng rượu vang có dạng khối tròn xoay với bán kính mặt đáy và mặt ở trên là 33 cm, bán kính mặt cắt ở chính giữa thùng là 43 cm. Chiều cao của thùng rượu là 112 cm, bao gồm phần thân thùng rượu, hai đế đỡ thùng rượu (mỗi đế cao 3 cm) và thùng rượu được ghép từ các thanh gỗ sồi với độ dày mỗi thanh gỗ là 3 cm (Hình a). Hình b mô phỏng phần bên trong thùng rượu có dạng một khối tròn xoay tạo thành khi quay một phần của parabol (P): y = ax2 + bc + c quanh trục hoành (mỗi đơn vị ứng với với 10 cm).
Thùng đó chứa được tối đa bao nhiêu lít rượu? (kết quả làm tròn đến hàng đơn vị).
Câu 4. Trong một khung lưới ô vuông gồm các hình lập phương, xét các đường thẳng đi qua hai nút lưới (mỗi nút lưới là đỉnh của hình lập phương), người ta đưa ra một cách kiểm tra độ lệch về phương của hai dường thẳng bằng cách gắn hệ tọa độ Oxyz vào khung lưới ô vuông và tìm vectơ chỉ phương của hai đường thẳng đó. Giả sử, đường thẳng a đi qua hai nút lưới M(1;1;2) và N(0;3;0), đường thẳng b đi qua hai nút lưới P(1;0;3) và Q(3;3;9). Sau khi làm tròn đến hàng đơn vị của độ thì góc giữa hai đường thẳng a và b bằng n° (n là số tự nhiên). Giá trị của n bằng bao nhiêu?
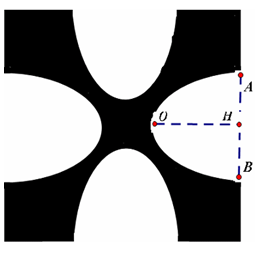
Câu 5. Khi đặt hệ tọa độ Oxyz vào không gian với đơn vị trên trục tính theo kilômét, người ta thấy rằng một không gian phủ sóng điện thoại có dạng một hình cầu (S) (tập hợp những điểm nằm trong và nằm trên mặt cầu tương ứng). Biết mặt cầu (S) có phương trình: . Khoảng cách xa nhất giữa hai vùng phủ sóng là bao nhiêu kilômét?
Câu 6. Tỉ lệ người dân đã tiêm vắc xin phòng bệnh A ở một địa phương là 65%. Trong số những người đã tiêm phòng, tỉ lệ mắc bệnh A là 5% còn trong số những người chưa tiêm, tỉ lệ mắc bệnh A là 17%. Gặp ngẫu nhiên một người ở địa phương đó. Biết rằng người đó mắc bệnh A. Khi đó xác suất người đó không tiêm vắc xin phòng bệnh A có dạng . Giá trị b - a là?
Xem thử Đề thi CK2 Toán 12 KNTT Xem thử Đề thi CK2 Toán 12 CTST Xem thử Đề thi CK2 Toán 12 CD
Lưu trữ: Đề thi Học kì 2 Toán 12 (sách cũ)


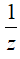 ?
? 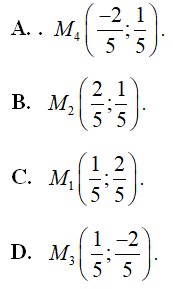
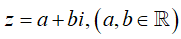 . Khẳng định nào sau đây là sai?
. Khẳng định nào sau đây là sai?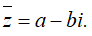
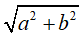 .
.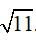
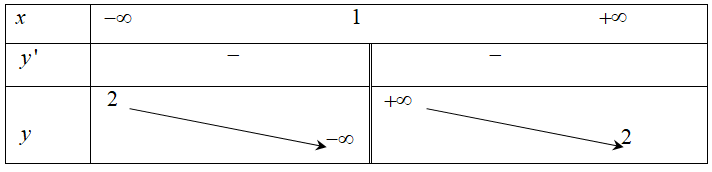
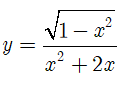 có bao nhiêu đường tiệm cận đứng?
có bao nhiêu đường tiệm cận đứng?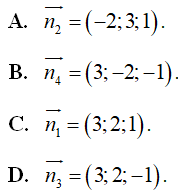
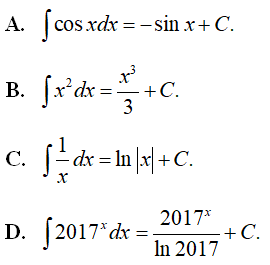
 . Đặt
. Đặt 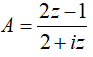 , khẳng định nào sau đây đúng?
, khẳng định nào sau đây đúng?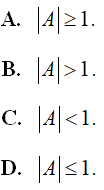
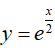 , trục hoành và hai đường thẳng x = 0 , x = 1 . Viết công thức tính thể tích V của khối tròn xoay khi quay hình phẳng (H) quanh trục Ox.
, trục hoành và hai đường thẳng x = 0 , x = 1 . Viết công thức tính thể tích V của khối tròn xoay khi quay hình phẳng (H) quanh trục Ox.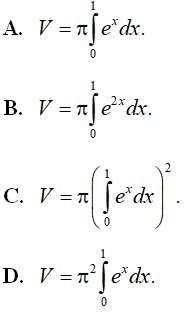
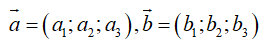 . Khẳng định nào sau đây sai ?
. Khẳng định nào sau đây sai ?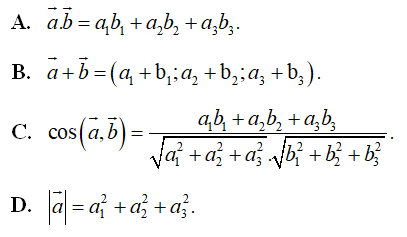
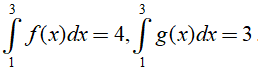 . Tính
. Tính 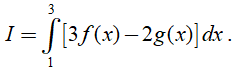 .
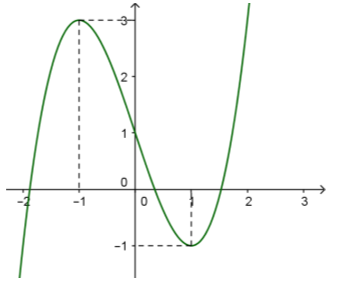
.
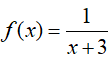 và F(-2) = 1 . Tính F(4) .
và F(-2) = 1 . Tính F(4) .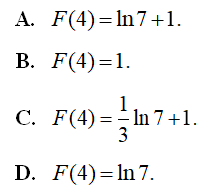
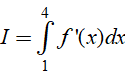
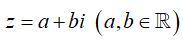 thỏa mãn
thỏa mãn 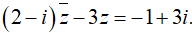 . Tính giá trị của biểu thức P = a - b
. Tính giá trị của biểu thức P = a - b 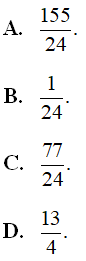
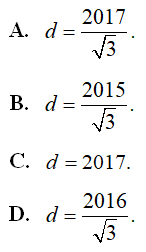
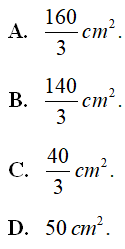
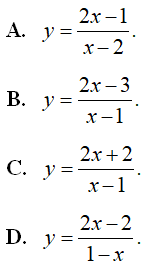
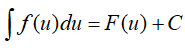 . Khẳng định nào sau đây là khẳng định đúng?
. Khẳng định nào sau đây là khẳng định đúng? 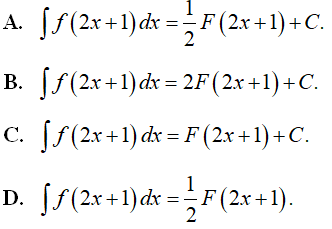
 , với a,b là các số nguyên. Tính S = a + b
, với a,b là các số nguyên. Tính S = a + b 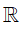 và
và 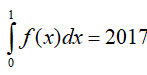 Tính
Tính 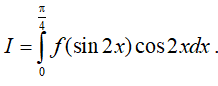 .
.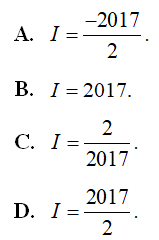
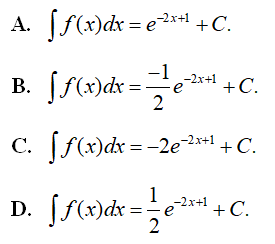
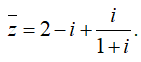 Tìm b?
Tìm b?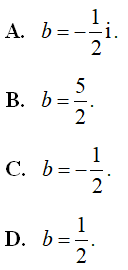
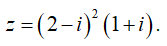
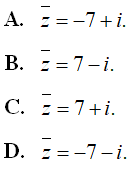
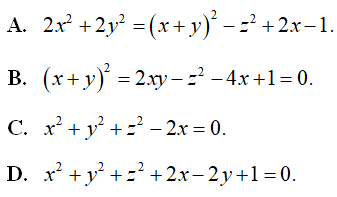
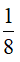 có bao nhiêu nghiệm?
có bao nhiêu nghiệm?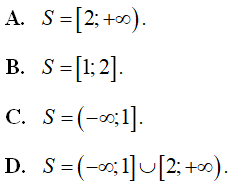
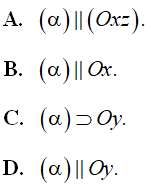
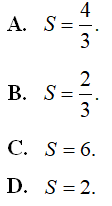
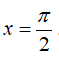 . Tính thể tích V của khối tròn xoay thu được khi quay hình (H) quanh trục Ox .
. Tính thể tích V của khối tròn xoay thu được khi quay hình (H) quanh trục Ox .
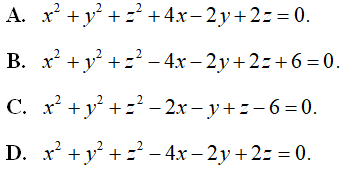
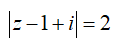 là
là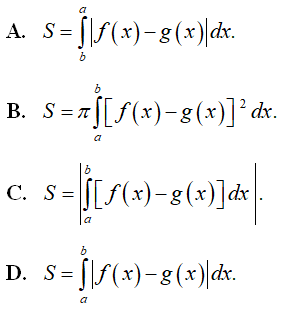
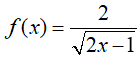 thỏa mãn F(1) = 3
thỏa mãn F(1) = 3