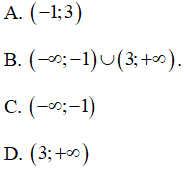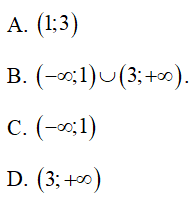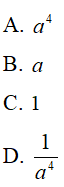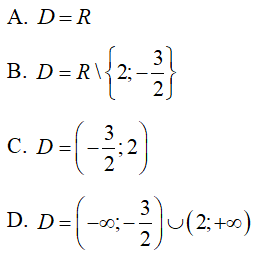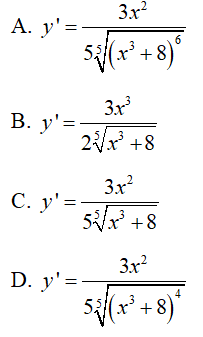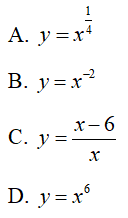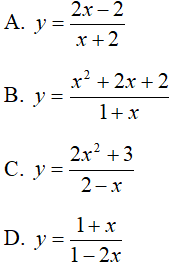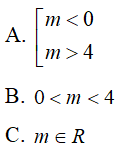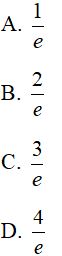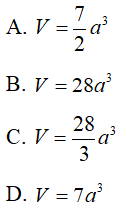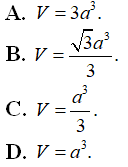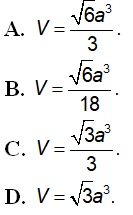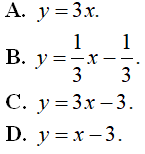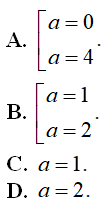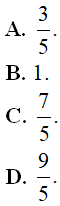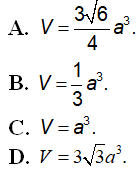Bộ đề thi Toán lớp 12 Học kì 1, Học kì 2 năm 2023 (60 đề)

---

Bộ đề thi Toán lớp 12 Học kì 1, Học kì 2 năm 2023 (60 đề)

Haylamdo biên soạn và sưu tầm Bộ đề thi Toán lớp 12 Học kì 1, Học kì 2 năm 2023 (60 đề) được tổng hợp chọn lọc từ đề thi môn Toán 12 của các trường trên cả nước sẽ giúp học sinh có kế hoạch ôn luyện từ đó đạt điểm cao trong các bài thi Toán lớp 12.

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Học kì 1

Năm học 2023 - 2022

Môn: Toán 12

Thời gian làm bài: 90 phút

Câu 1 : Hàm số y = x³ - 3x² - 9x nghịch biến trên các khoảng nào sau đây?

Câu 2 : Hàm số 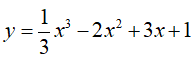đồng biến trên các khoảng nào sau đây?

Câu 3 : Rút gọn biểu thức: 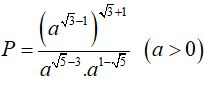. Kết quả là:

Câu 4 : Điểm cực đại của hàm số y = x(3 - x)² là những điểm nào sau đây?

A. (1;3)

B. (3;0)

C. (1;4)

D. Đáp án khác

Câu 5 : Giá trị lớn nhất của hàm số y = x³ - 3x² - 9x + 35 trên đoạn [-4 ; 4] bằng. Chọn 1 câu đúng.

A. 8

B. 15

C. -41

D. 40

Câu 6 : Tập xác định của hàm số y = (2x² - x - 6)^-5 là:

Câu 7 : Tính thể tích V của hình hộp chử nhật ABCD.A'B'C'D' , biết AB = 3cm, AD = 6cm , CC' = 9cm là:

A. V = 18cm

B. V = 18cm³

C. v = 81cm³

D. V = 162cm³

Câu 8 : Để tìm các điểm cực trị của hàm số f(x) = 4x⁵ - 5x⁴ một học sinh lập luận qua ba bước sau:

Bước 1: Hàm số có tập xác định D = R

Ta có: f'(x) = 20x³(x - 1)

f'(x) = 0 ⇔ x³(x - 1) = 0 ⇔ x = 0 hoặc x = 1

Bước 2: Đạo hàm cấp hai f''(x) = 20x²(4x - 3)

Suy ra: f''(0) 0 , f''(1) = 20 > 0

Bước 3: Từ các kết quả trên kết luận:

Hàm số không đạt cực trị tại x = 0

Hàm số đạt cực tiểu tại x = 1

Vậy hàm số chỉ có một cực tiểu duy nhất, đạt tại điểm x = 1

A. Lập luận hoàn toàn đúng

B. Sai từ bước 1

C. Sai từ bước 2

D. Sai từ bước 3

Câu 9 : Cho hàm số y = x³ - 3x² - 9x + 4 . Nếu hàm số đạt cực đại và cực tiểu thì tích số y_CD, y_CT bằng:

A. 25

B. Hàm số không đạt cực đại và cực tiểu.

C. -207

D. -82

Câu 10 : Đạo hàm của hàm số 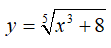là:

Câu 11 : Tìm giá trị lớn nhất của hàm số 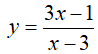trên đoạn [0;2]

Câu 12 : Giá trị nhỏ nhất của hàm số 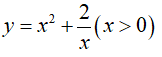là:

A. 1

B. 2

C. 3

D. 4

Câu 13 : Hàm số nào sau đây nghịch biến trên khoảng (0; +∞) ?

Câu 14 : Cho hàm số 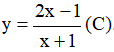Các phát biểu sau, phát biểu nào Sai ?

A. Hàm số luôn đồng biến trên từng khoảng của tập xác định của nó;

B. Đồ thị hàm số có tiệm cận ngang là đường thẳng y = 2 .

C. Đồ thị hàm số có tiệm cận đứng là đường thẳng x = 1 ;

D. Đồ thị hàm số (C) có giao điểm với Oy tại điểm có hoành độ là ;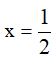

Câu 15 : Đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số nào sao đây? Chọn 1 câu đúng.

Câu 16 : Biết log2 = 2, log3 = b . Tính log45 theo a và b .

A. 2b + a + 1

B. 2b - a + 1

C. 15b

D. a - 2b + 1

Câu 17 : Đồ thị sau đây là của hàm số nào ? Chọn 1 câu đúng.

A.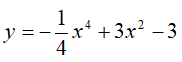

B. y = x⁴ - 2x² - 3

C. y = x⁴ + 2x² - 3

D. y = x⁴ - 3x² - 3

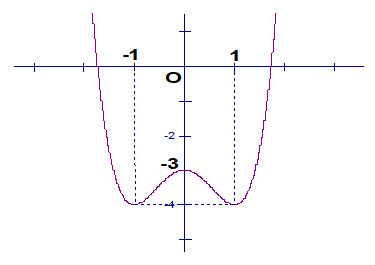
Câu 18 : Tìm m để phương trình x³ + 3x² - 2 = m + 1 có 3 nghiệm phân biệt.

A. -2 < m < 0

B. 2 < m < 4

C. -3 < m < 1

D. 0 < m < 3

Câu 19 : Hàm số y = log₅^{(4x - x)2} có tập xác định là :

A. (2;6)

B. (0;4)

C. (0;+∞)

D. R

Câu 20 : Có bao nhiêu loại khối đa diện đều?

A. 3

B. Vô số

C. 5

D. 20

Câu 21 : Cho hàm số 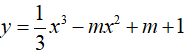. Tìm m để hàm số đạt cực đại và cực tiểu. thỏa mãn x²_A + x²_B = 2 :

A. m = ±1

B. m ≠ 0

C. m = 2

D. m = ± 3

Câu 22 : Đường thẳng Δ: y = -x + m cắt đồ thị hàm số 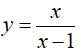tại hai điểm phân biệt, ứng với các giá trị của là:

D. Kết quả khác

Câu 23 : Cho f(x)= ln²x . Đạo hàm f'(e) bằng :

Câu 24 : Cho đường cong 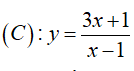. Tích số các khoảng cách từ một điểm bất kỳ trên (C) đến hai đường tiệm cận của (C) bằng:

A. 2

B. 3

C. 4

D. Kết quả khác

Câu 25 : Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau; AB = 6a, AC = 7a và AD = 4a. Tính thể tích V của tứ diện ABCD.

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa kì 1

Năm học 2023 - 2022

Môn: Toán 12

Thời gian làm bài: 90 phút

Câu 1 : Cho hàm số y = x³ - 3m²x² - m³ có đồ thị (C) . Tìm tất cả các giá trị thực của tham số m để tiếp tuyến của đồ thị (C) tại điểm có hoành độ x₀ = 1 song song với đường thẳng d = -3x

A. m = 1

B. m = -1

C.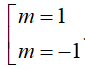

D. Không có giá trị của m

Câu 2 : Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = x⁴ - 2x² + 3 trên [0;2] là:

A. M = 11 , m = 3

B. M = 5 , m = 2

C. M = 3 , m = 2

D. M = 11 , m = 2

Câu 3 : Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a và thể tích bằng a³ Tính chiều cao h của hình chóp đã cho.

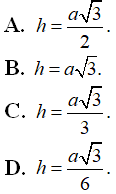
Câu 4 : Hình đa diện nào dưới đây không có tâm đối xứng ?

A. Hình tứ diện đều.

B. Hình lăng trụ tam giác đều.

C. Hình bát diện đều.

D. Hình lập phương.

Câu 5 : Số đường tiệm cận của đồ thị hàm số 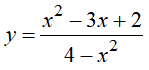là:

A. 4.

B. 1.

C. 2.

D. 3.

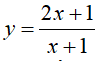
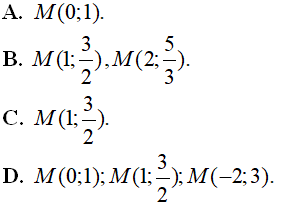
Câu 6 : Cho hàm số có đồ thị (C). Tìm các điểm M trên đồ thị (C) sao cho khoảng cách từ hai điểm A(2;4) và B(-4;-2) đến tiếp tuyến của (C) tại M là bằng nhau

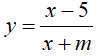
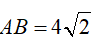
Câu 7 : Tổng các giá trị thực của tham số m sao cho đường thẳng y = x cắt đồ thị hàm số tại hai điểm A và B sao cho là

A. 2

B. 5

C. 7

D. 9

Câu 8 : Tìm tất cả các giá trị thực của tham số m để đường thẳng d: y = -x + m cắt đồ thị hàm số 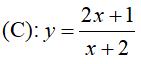tại hai điểm phân biệt

A. -1 < m < 4

B.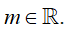

C. m = 4

D. -1 < hoặc m > 4

Câu 9 : Tìm số cạnh của hình mười hai mặt đều.

A. 20.

B. 12.

C. 30.

D. 16.

Câu 10 : Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm của tam giác BCD Tính thể tích V của khối chóp A.GBC

A. V = 6

B. V = 4

C. V = 5

D. V = 3

Câu 11 : Cho hàm số y = f(x) có đạo hàm f'(x) = x² + 1 Mệnh đề nào dưới đây đúng ?

A. Hàm số nghịch biến trên khoảng (-1;1)

B. Hàm số nghịch biến trên khoảng (1; +∞)

C. Hàm số nghịch biến trên khoảng (-∞;0)

D. Hàm số đồng biến trên khoảng (-∞ ;+∞)

Câu 12 : Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x⁴ - (m + 1)x² + m cắt trục hoành tại bốn điểm phân biệt có tổng bình phương các hoành độ bằng 8

A. m = 1

B.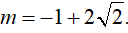

C. m = 7

D. m = 3

Câu 13 : Cho khối chóp S.ABCD có đáy là hình chữ nhật, AB = A, 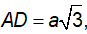SA vuông góc với đáy và mặt phẳng (SBC) tạo với đáy một góc 60⁰ Tính thể tích V của khối chóp đã cho.

Câu 14 : Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt đáy, SD tạo với mặt phẳng (SAB) một góc bằng 30⁰ . Tính thể tích V của khối chóp

Câu 15 : Cho hàm số 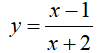có đồ thị (C). Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là:

Câu 16 : Để đường cong 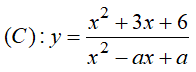có đúng 1 đường tiệm cận đứng thì giá trị của a là

Câu 17 : Mặt phẳng (AB'C') chia khối lăng trụ ABC.A'B'C' thành các khối đa diện nào ?

A. Một khối chóp tam giác và một khối chóp tứ giác.

B. Hai khối chóp tam giác.

C. Một khối chóp tam giác và một khối chóp ngũ giác.

D. Hai khối chóp tứ giác.

Câu 18 : Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng ?

A. 4 mặt phẳng.

B. 1 mặt phẳng.

C. 3 mặt phẳng.

D. 2 mặt phẳng.

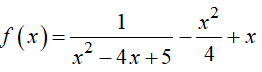
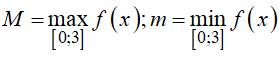
Câu 19 : Cho . Gọi , khi đó: M - m bằng

Câu 20 : Cho hàm số 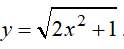. Mệnh đề nào dưới đây đúng ?

A. Hàm số nghịch biến trên khoảng (0;+∞)

B. Hàm số đồng biến trên khoảng (-∞;0)

C. Hàm số nghịch biến trên khoảng (-1;1)

D. Hàm số đồng biến trên khoảng (0;+∞)

Câu 21 : Tính thể tích V của khối lập phương ABCD.A'B'C'D' , biết AC' =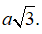

Câu 22 : Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Biết SA vuông góc với mặt phẳng đáy và thể tích của khối chóp S.ABC là V = 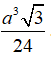. Tìm α là góc hợp giữa hai mặt phẳng (ABC) và (SBC).

A. α = 45^o

B. α = 30^o

C. α = 90^o

D. α = 60^o

Câu 23 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Biết thể tích của khối chóp S.ABCD theo a là V = 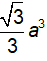. Góc α giữa đường thẳng SD và mặt phẳng (SAB) là bao nhiêu độ ?

A. α = 90^o

B. α = 60^o

C. α = 45^o

D. α = 30^o

Câu 24 : Số điểm cực đại của đồ thị hàm số 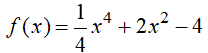là:

A. 1

B. 3

C. 2

D. 0

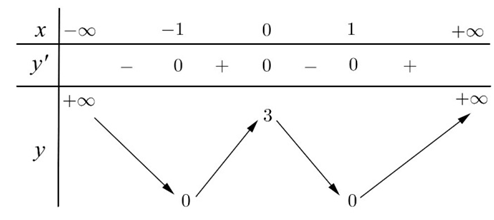
Câu 25 : Cho hàm số y = f(x) có bảng biến thiên như sau

Mệnh đề nào dưới đây sai ?

A. Hàm số có giá trị cực đại bằng 0

B. Hàm số có ba điểm cực trị.

C. Hàm số có hai điểm cực tiểu.

D. Hàm số có giá trị cực đại bằng 3.

................