Tính các giá trị lượng giác của góc α, nếu cosα = 4/13 và 0 < α < π/2

Bài 2: Giá trị lượng giác của một cung

Bài 4 trang 148 Toán 10: Tính các giá trị lượng giác của góc α, nếu

a) cosα = 4/13 và 0 < α < π/2

b) sinα = -0,7và π < α < 3π/2

c) tanα = (-5)/17 và π/2 < α < π

d) cotα = -3 và 3π/2 < α < 2π

Trả lời

a) Vì 0 < α < π/2 nên sin α > 0; tan α > 0; cot α > 0

* Từ cos2α + sin2α = 1, ta có:

(4/13)² + sin2 α = 1 ⇔ sin2 α = 1 – 16/169

⇔ sin α = (3√17)/13

* Từ tan α = sinα/cosα, ta có tan α = (3√17)/4

* Từ cot α = cosα/sinα, ta có cot α = 4/(3√17)

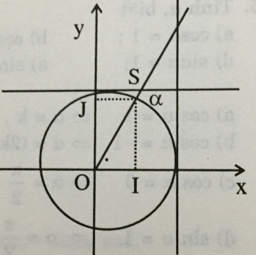
b) Vì π < α < 3π/2 nên cosα < 0;tanα > 0;cotα>0

* Từ cos² α + sin² α = 1, ta có:

cos2 α = 1 – (0,7)² = 0,51 = 51/100 => cos α = (-√51)/10

* Từ tan α=(cos α)/(sin α) ta có tan α=(-0,7.10)/(-√51)

=> tan α = (7√51)/51

* Từ cot α = 1/(tan α), ta có tan α=√51/7

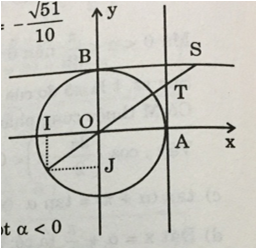
c) Vì π/2 < α < π, nên cos α < 0; sin α > 0; cot α < 0

* Từ cot α.tan α = 1, ta có cot α = (-7)/15

* Từ cos²α = 1/(1 + tan² α) ta có cos²α=1/(1+(-15/7)² )

=> cos α = (-7)/√274

* Từ sin2α=1/(1+cos² α), ta có sin α=15/√274

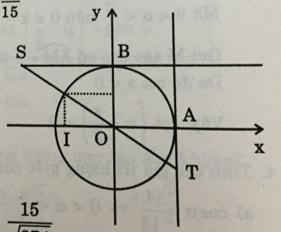
d) Vì 3π/2 < α < 2π nên sin α < 0; cos α > 0; tan α < 0

Tương tự ta có kết quả sin α = (-1)/√10;cosα = 3/√(10 );tanα = -1/3