Cho phương trình 3x^2 – 2(m + 1)x + 3m – 5 = 0

Bài 2: Phương trình quy về phương trình bậc nhất, bậc hai

Bài 8 trang 63 Toán 10: Cho phương trình 3x₂ – 2(m + 1)x + 3m – 5 = 0

Xác định m để phương trình có một nghiệm gấp ba nghiệm kia. Tính các nghiệm trong trường hợp đó.

Trả lời

Theo định lí Vi-ét, ta có:

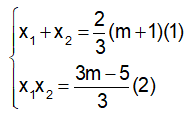
Theo giả thuyết ta có x₁ = 3x₂ (3)

* Để có x₁ và x₂ điều kiện là:

Δ’ = (m + 1)² + 15 – 9m = m2 – 7m + 16 > 0, mọi x ∈ R.

* Từ (1) và (3) ta có: 4x₂ = 2/3(m + 1) ⇔ x₂ = (m+1)/6 (4)

Từ (3) và (4) ta có: x₁ = (m+1)/2 (5)

* Thay x₁ và x₂ ở (5) và (4) vào (2), ta có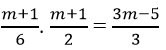

⇔ (m + 1)² = 4(3m – 5) ⇔ m2 – 10m + 21 = 0⇔ m =3; m =7

* Khi m = 3 thì x₁ = 2; x₂ = 2/3

* Khi m = 7 thì x₁ = 4; x₂ = 4/3