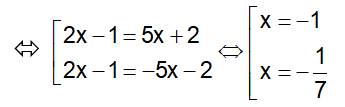Giải các phương trình |3x-2| = 2x + 3

---

Bài 2: Phương trình quy về phương trình bậc nhất, bậc hai

Bài 6 trang 62 Toán 10: Giải các phương trình:

a) |3x-2| = 2x + 3

b) |2x-1|=|-5x-2|

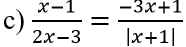
d) |2x+5| = x² + 5x + 1

Trả lời

a) |3x-2| = 2x + 3

Cách 1

* Tập xác định: 2x + 3 ≥ 0 ⇔ x ≥(-3)/2 (*)

* Loại bỏ dấu giá trị tuyệt đối

Ta có: |3x-2| = 3x – 2 khi x ≥2/3

= -3x + 2 khi x < 2/3

Có hai trường hợp:

* Khi x ≥2/3 thì (1) ⇔ 3x – 2 = 2x + 3 ⇔ x = 5 (nhận, do (*))

* Khi x < 2/3 thì (1) ⇔ -3x + 2 = 2x + 3⇔ 5x = -1 ⇔ x = (-1)/5 (nhận, do (*))

Tóm lại, (1) có tập nghiệm: T = {5; (-1)/5}

Cách 2

* Tập xác định: x ≥(-3)/2

* Bình phương hai vế: (3x – 2)2 = (2x + 3)2

⇔ 5x² – 24x – 5 = 0 ⇔ x = 5; x = (-1)/5

thử lại: |3x-2|=|3.5-2| = 13

2x + 3 = 2.5 + 3 = 13

⇔ x = 5 (nhận)

|3x-2|=|3.(-1/5)-2|=|-13/5|=13/5

2x + 3 = 2(- 1/5 ) + 3 = 13/5

⇒ x = - 1/5 (nhận)

Vậy T = {5; - 1/5}

Cách 2

* Tập xác định: x ≥ (-3)/2

* Bình phương hai vế: (3x – 2)2 = (2x + 3)2

⇔ 5x² – 24x – 5 = 0 ⇔ x = 5; x = (-1)/5

thử lại: |3x-2|=|3.5-2|=13

2x + 3 = 2.5 + 3 = 13

⇒ x = 5 (nhận)

|3x-2|=3.(-1/5)-2=|-13/5|=13/5

2x + 3 = 2.(-1/5)+3=13/5

⇒ x = - 1/5 (nhận)

Vậy T = {5; - 1/5}

b) |2x-1|=|-5x-2| ⇔ 2x – 1 = ± (5x + 2)

⇔

Vậy T = {-1; -1/7}

(1)

* Tập xác định:

2x – 3 ≠ 0 ⇔ x ≠3/2

x + 1 ≠ 0 ⇔ x ≠ -1

Vậy x ≠3/2 và x ≠ -1

* Khi x > -1, ta có:

(1) ⇔ ⇔ x² + 1 = (2x – 3)(-3x + 1)

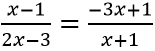
⇔ 7x² – 11x + 2 = 0 ⇔ 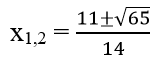(nhận, do thỏa x > -1)

* Khi x < -1, ta có:

(1) ⇔ ⇔ (x – 1)(-1 – x) = (2x – 3)(-3x + 1)

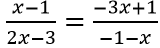
⇔ -x – x² + 1 + x = -6x² + 2x + 9x – 3

⇔ 5x² + 11x + 2 = 0 ⇔ 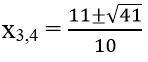(loại, do không thỏa x < -1)

Vậy T = {(11±√41)/10}

d) |2x+5| = x² + 5x + 1 (1)

Khi x ≥ (-5)/2 ta có:

2x + 5 = x² + 5x + 1 ⇔ x² + 3x – 4 = 0 ⇔ x1 = 1; x² = -4 (loại)

Khi x < -5/2 ta có:

-2x – 5 = x² + 5x + 1 ⇔ x² + 7x + 6 = 0 ⇔ x1 = -1 (loại); x² = -6

Thử lại ta thấy phương trình (1) đã cho có hai nghiệm là x = 1; x = -6