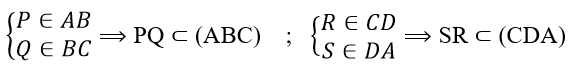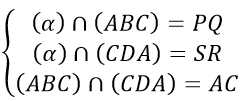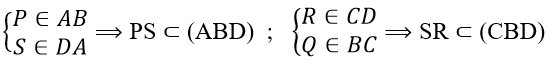Cho tứ diện ABCD. Gọi P, Q, R và S là bốn điểm lần lượt lấy trên 4 cạnh AB, BC

Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song

Bài 1 trang 59 Toán 11: Cho tứ diện ABCD. Gọi P, Q, R và S là bốn điểm lần lượt lấy trên 4 cạnh AB, BC, CD và DA. Chứng minh rằng nếu 4 điểm P, Q, R và S đồng phẳng thì:

a) Ba đường thẳng PQ,SR và AC song song hoặc đồng quy

b) Ba đường thẳng PS, RQ và BD hoặc song song hoặc đồng quy

Trả lời

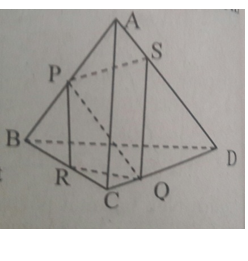
Do P, Q, R, S đồng phẳng nên chúng cùng một mp (α)

a) Ta có :

Khi đó

⇒ Ba đường thẳng PQ, SR và AC song song hoặc đồng quy

b) Ta có :

Khi đó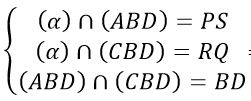

⇒ Ba đường thẳng PS, RQ và BD song song hoặc đồng quy.