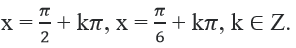Giải các phương trình sau: 2sin^2 x + sinx.cosx – 3cos^2 x = 0

Bài 3: Một số phương trình lượng giác thường gặp

Bài 4 trang 37 Toán 11: Giải các phương trình sau:

a) 2sin²x + sinx. cosx – 3cos²x = 0;

b) 3sin²x – 4sinx . cosx + 5cos²x = 2;

c) sin²x + sin2x – 2cos²x = 1/2;

d) 2cos²x - 3√3sin2x – 4sin²x = –4 .

Trả lời

a) Nhận thấy cosx = 0 không là nghiệm của phương trình này. Do đó chia hai vế cho cos²x ta được:

2tan²x + tanx – 3 = 0

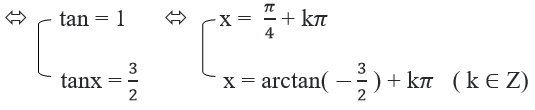
b) Nhận thấy cosx = 0 không là nghiệm của phương trình nên chia hai vế phương trình cho cos²x ta được: 3tan²x – 4tanx + 5= 2(1 + tan²x)

⇔ tan²x – 4tanx + 3 = 0

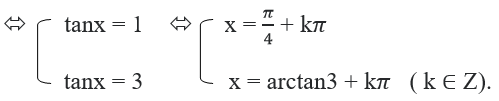
c) sin²x + sin2x – 2cos²x = 1/2. Nhận thấy cosx = 0 không là nghiệm của phương trình. Chia hai vế của phương trình cho cos²x, ta được:

tan²x + 2tanx – 2 = 1/2 (1 + tan²x) ⇔ tan²x + 4tanx – 5 = 0

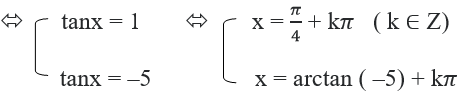
d) 2cos²x - 3√3sin2x – 4sin²x = –4

Với cosx = 0 ⇔ x = π/2 + kπ, khi đó phương trình trở thành

- 4sin²x = - 4 ⇔ sin²x = 1 luôn đúng => x = π/2 + kπ , k ∈ Z

Với cosx ≠ 0, chia hai vế cho cos²x, ta được:

2 - 6√3tanx – 4tan²x = –4(1 + tan²x) ⇔ 6√3tanx = 6

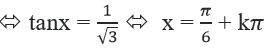
Vậy phương trình có nghiệm: