Cho góc xOy khác góc bẹt. Lấy các điểm A, B thuộc tia Ox sao cho OA < OB

Giải bài tập Toán lớp 7 Luyện tập về ba trường hợp bằng nhau của tam giác (trang 125)

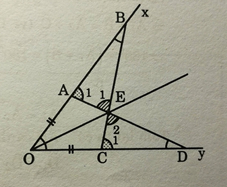
Bài 43 trang 125 Toán lớp 7 Tập 1: Cho góc xOy khác góc bẹt. Lấy các điểm A, B thuộc tia Ox sao cho OA < OB.

Lấy các điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC.

Chứng minh rằng:

a) AD = BC;

b) ΔEAB = ΔECD;

c )OE là tia phân giác của xOy.

Trả lời

a) Chứng minh AD = BC

Hai tam giác ΔOAD và ΔOCB có: OA = OC(gt)

O chung

OD = OB(gt)

Do đó ΔOAD = ΔOCB(c.g.c)

Suy ra AD = BC (đpcm)

b) Chứng minh ΔEAB = ΔECD.

ΔOAD = ΔOCB(cmt) ⇒ B = D (1)

Ta có E₁ = E₂ (đối đỉnh)

⇒ B + E₁ = D + E₂ ⇒ 180⁰ - (B + E₁) = 180⁰ - (D + E₂) (2)

Còn có OB = OD và OA = OC ⇒ OB - OA = OD - OC ⇔ AB = CD (3)

Tóm lại hai tam giác EAB và ECD có B = D (1) ; AB = CD (3) ; A₁ = C₁ (2)

⇒ ΔEAB = ΔECD (g.c.g) (đpcm)

c) OE là tia phân giác của góc xOy

Hai tam giác OAE và OCE có OA = OC (gt) ; EA = EC (do ΔEAB = ΔECD) ; OE cạnh chung

Do đó ΔOAE = ΔOCE (c.c.c)

Suy ra AOE = COE mà OE nằm giữa OA và OC.

Vậy OE là tia phân giác của góc xOy.