Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M, trên tia đối của

---

Toán 7 Ôn tập chương 2 (Câu hỏi - Bài tập)

Bài 70 trang 141 Toán lớp 7 Tập 1: Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM = CN.

a) Chứng minh rằng tam giác AMN là tam giác cân.

b) Kẻ BH ⊥ AM (H ∈ AM), kẻ CK ⊥ AN (K ∈ AN). Chứng minh rằng BH = CK.

c) Chứng minh rằng AH = AK.

d) Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì? Vì sao ?

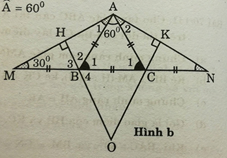
e) Khi BAC = 60⁰ và BM = CN = BC, hãy tính số đo các góc của tam giác AMN và xác định dạnh của tam giác OBC.

Trả lời

   

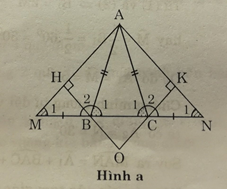
a) Tam giác AMN cân

Ta có:

AB = AC (ΔABC cân tại A)

ABM = ACN (do B₁ = C₁)

BM = CN (gt)

⇒ ΔABM = ΔACN (c.g.c)

⇒ AM = AN (hai cạnh tương ứng)

Vậy ΔAMN là tam giác cân ở A.

b) Chứng minh BH = CK

Hai tam giác vuông BHM (H = 90⁰) và CKN (K = 90⁰) có:

BM = CN (gt)

M₁ = N₁ (do tam giác AMN cân tại A)

Do đó ΔBHM = ΔCKN ⇒ BH = CK (đpcm)

c) Chứng minh AH = AK

Ta có AM = AN (tam giác AMN cân tại A) (1)

MH = NK (ΔBHM = ΔCKN) (2).

Trừ (1) và (2) vế theo vế ⇒ AH = AK

Vậy AH = AK (đpcm)

d) Dạng của tam giác OBC

ΔBHM = ΔCKN (cmt) ⇒ MBH = NCK

Mà MBH = CBO (đối đỉnh) và NCK = BCO (đối đỉnh)

⇒ COB = BCO (đối đỉnh) do đó ∆OBC là tam giác cân tại O (đpcm)

e) Số đo các góc của tam giác AMN (h.b)

Tam giác ABC cân tại A và có A = 60⁰ nên là tam giác đều

⇒ B₁ = C₁ = 60⁰

Ta có BM = BA (vì cùng bằng BC)

⇒ tam giác ABM cân tại B

⇒ A₁ = M (1)

Còn có B₁ = A₁ + M (góc ngoài của tam giác ABM) (2)

Từ (1) và (2) ⇒ B₁ = 2M hay M = 30⁰

Do đó A₁ = M = 30⁰

Chứng minh tương tự đối với tam giác CAN

Ta có A₂ = N = 30⁰

Suy ra MAN = A₁ + BAC + A₂ = 30⁰ + 60⁰ + 30⁰ = 120⁰

Vậy các góc của tam giác MAN là A = 120⁰ ; M = N = 30⁰

Dạng của tam giác OBC

Ta có tam giác OBC là tam giác cân (cmt)

Trong tam giác vuông MBH có:

H = 90⁰ ; M = 30⁰ ⇒ B₃ = 60⁰

Do đó B₄ = B₃ = 60⁰ (đối đỉnh)

Vậy tam giác OBC là tam giác đều (tam giác cân có một góc 60⁰)