Giải các phương trình 1/x-1 - 3x^2/x^3-1 = 2x/x^2 + x + 1

Luyện tập (trang 22-23)

Bài 31 trang 23 Toán 8 Tập 2: Giải các phương trình:

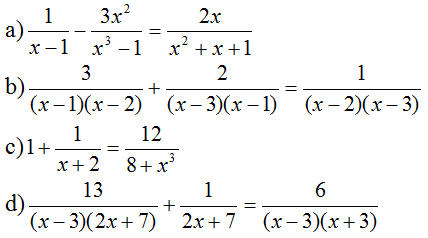
Trả lời

a) ĐKXĐ x ≠ 1. (MTC x³ -1 = (x- 1) (x² + x +1))

(1) ⇔ x² + x + 1 - 3x² = 2x(x-1)

⇔ -4x² + 3x +1 = 0

⇔ -4x² – x + 4x + 1 = 0

⇔ -x(4x+ 1) + (4x +1 ) = 0

⇔ (4x+1) (1-x) = 0

⇔ 4x +1 = 0 hoặc 1- x = 0

⇔ x = -1/4 (nhận) hoặc x = 1 (loại)

Vậy S = {-1/4}

b) ĐKXĐ x ≠ 1, x ≠ 2, x ≠ 3

(2) ⇔ 3(x-3) + 2 (x-2) = x- 1 ⇔ 4x = 12 ⇔ x = 3 (loại)

Vậy (2) vô nghiệm

c) ĐKXĐ x ≠ -2

Ta có MTC = x³ + 8 = (x +2 ) ( x² -2x + 4)

(3) ⇔ x³ + 8 + x² – 2x + 4 = 12 ⇔ x³ + x² -2x = 0

⇔ x³ – x² + 2x² – 2x = 0

⇔ x²( x-1) + 2x(x-1) = 0

⇔x(x-1)(x+2) = 0

⇔ x = 0 hoặc x = 1 hoặc x = -2(loại)

Vậy S = {0,1}

d) ĐKXĐ x ≠ 3, x ≠ -3, x ≠ -7/2 . MTC = (x – 3) ( x+3) (2x + 7)

(4) ⇔ 13(x +3) + (x-3)(x+3) = 6(2x +7)

⇔ x² + 13x + 30 =12x + 42

⇔ x² + x – 12 = 0

⇔x² + 4x -3x – 12 = 0

⇔x(x+ 4) -3 (x +4) = 0

⇔ (x+4) (x-3) = 0

⇔ x = -4 hoặc x = 3(loại)

Vậy S = {-4}