Cho tam giác ABC, D là một điểm nằm giữa B và C

Luyện tập (trang 109)

Bài 84 trang 109 Toán 8 Tập 1: Cho tam giác ABC, D là một điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự ở E và F

a) Tứ giác AEDF là hình gì? Vì sao?

b) Điểm D ở vị trị nào trên cạnh BC thì tứ giác AEDF la hình thoi

c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì. Điểm D ở vi trí nào trên cạnh BC thì tứ giác AEDF là hình vông

Trả lời

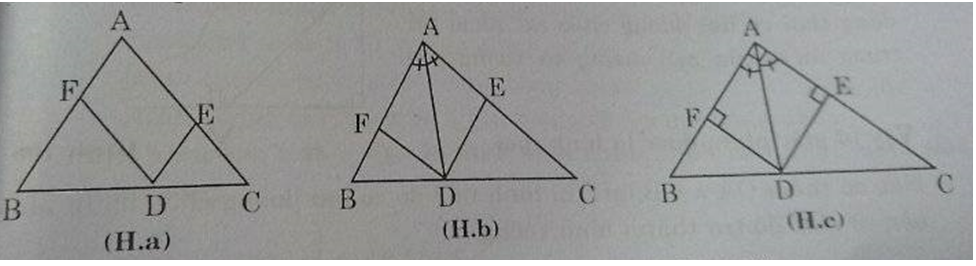
a) Tứ giác AEDF có AE // DG (gt) và DE // FA (gt)

Vậy AEDF là hình bình hành (định nghĩa) (H.a)

b) Để hình bình hành AEDF là hình thoi thì đường chéo AD là phân giác góc A. Vậy điểm D là giao điểm phân giác góc A với cạnh BC thì AEDF là hình thoi (H.b)

c) Nếu ABC vuông tại A thì ABCD là hình chữ nhật (H.c). Trong câu b ta thấy, nếu AD là đường phân giác trong góc A (D ∈ BC) thì AEDF là hình thoi và nếu tam giác ABC vuông tại Athif hình thoi AEDF trở thành hình vuông. Vậy để tứ giác AEDF là hình vuông thì tam giác ABC vuông tại A và D là giao điểm của phân giác góc A và BC

Tóm lại Tam giác ABC có D ∈ BC; DE // AC ; DF //AB

a) DE // AD và DF // AB         b) Hình bình hành         c) Hình thoi AEDF

⇒AEDF là hình bình hành          AEDF + ∠A1 = ∠A2          + ∠BAC = 90°

                                                     ⇒AEDF là hình thoi         ⇒AEDF là hình vuông