Bài 10 trang 104 Toán 9 Tập 1

Bài 2: Đường kính và dây của đường tròn

Bài 10 trang 104 Toán 9 Tập 1: Cho tam giác ABC, các đường cao BD và CE.

Chứng minh rằng:

a) Bốn điểm B, E, D, C cùng thuộc một đường tròn.

b) DE < BC.

Bài giải:

a) B, E, D, C cùng thuộc một đường tròn:

Gọi O là trung điểm của BC.

⇒ OD và OE là trung tuyến ứng với cạnh huyền BC của các tam giác vuông BDC và BEC.

⇒ OD = OE = OB = OC = 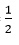BC

⇒ B, D, E, C cách đều điểm O.

Do đó B, D, E, C cùng thuộc đường tròn tâm O đường kính BC.

b) DE < BC

Ta có: DE là một dây cửa (O) không đi qua tâm.

        BC là đường kính của (O)

        Căn cứ vào định lý 1: Đường kính là dây lớn nhất của đường tròn

Do đó: DE < BC

Ghi chú: Ta có B, O, C thẳng hàng

⇒ ∠BOC + ∠EOD + ∠DOC = 180° ⇒ ∠EOD < 180°

⇒ Ba điểm E, O , D không thẳng hàng

Do đó dây DE không đi qua tâm O.