Bài 11 trang 104 Toán 9 Tập 1

Bài 2: Đường kính và dây của đường tròn

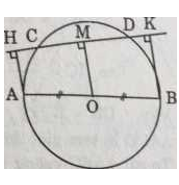
Bài 11 trang 104 Toán 9 Tập 1: Cho đường tròn (O) đường kính AB, dây CD không cắt đường kính AB. Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng CH = DK

Gợi ý: Kẻ OM vuông góc với CD.

Bài giải:

        Nhắc lại: Trong một song với hai đáy thì đi qua trung điểm của cạnh bên thứ hai.

        CH = DK

Ta có: AH // BK (cùng vuông góc với CD) và ∠H = ∠K = 90° (gt)

⇒ Tứ giác ABKH là hình thang vuông.

Kẻ OM vuông góc với CD.

Trong hình thang ABKH có:

OA = OB = bán kính

OM // AH // BK (cùng vuông góc với CD)

⇒ MH = MK     (1)

Ta có: OM vuông góc với CD

⇒ MC = MD (đường kính vuông góc với dây thì đi qua trung điểm của dây ấy     (2)

Trừ (1) và (2) vế theo vế ta có:

MH - MC = MK - MD

⇔ HC = DK

Vậy HC = DK