Bài 12 trang 106 Toán 9 Tập 1

Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây

Bài 12 trang 106 Toán 9 Tập 1: Cho đường tròn tâm O bán kính 5cm, dây AB bằng 8cm.

a) Tính khoảng cách từ tâm O đến dây AB.

b) Gọi I là điểm thuộc dây AB sao cho AI = 1 cm. Kẻ dây CD đi qua I và vuông góc với AB. Chứng minh rằng CD = AB

Bài giải:

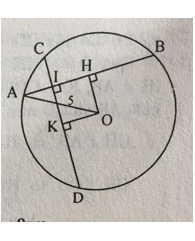
a) Khoảng cách từ tâm O đến dây AB:

Gọi OH là khoảng cách từ O đến AB

⇒ OH vuông góc với AB

⇒ HA = HB = 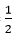AB = 4cm

Từ tam giác vuông OAH ta có:

OH² = OA² - AH² = 5² - 4² = 9 ⇒ OH = 3cm

Vậy khoảng cách từ tâm O đến dây AB bằng 3cm.

b) CD = AB:

Kẻ OK vuông góc với CD, ta có: ∠H = ∠I = ∠K = 90°

⇒ OHIK là hình chữ nhật     (1)

Ta có: HI = HA - AI = 4 - 1 = 3(cm)

và OH = 3cm (cmt) ⇒ OH = HI = 3cm     (2)

Từ (1) và (2) suy ra: OHIK là hình vuông ⇒ OK = OH = 3cm

Do đó: CD = AB