Bài 13 trang 106 Toán 9 Tập 1

Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây

Bài 13 trang 106 Toán 9 Tập 1: Cho đường tròn (O) có các dây AB và CD bằng nhau, các tia AB và CD cắt nhau tại điểm E nàm bên ngoài đường tròn. Gọi H và K theo thứ bự là trung điểm của AB và CD. Chứng minh rằng :

a) EH = EK;

b) EA = EC

Bài giải:

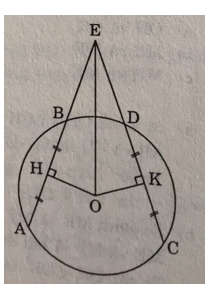
a) EH = EK

Ta có: HA = HB (gt) ⇒ OH vuông góc vớiAB

        KC = KD (gt) ⇒ OK vuông góc với CD

        AB = CD (gt) ⇒ OH = OK

Hai tam giác vuông OHE và OKE bằng nhau vì có OE chung và OH = OK

⇒ EH = EK

b) EA= EC

Do AB = AC ⇒ HA = KC

⇒ EH + HA = EK + KC

⇔ EA = EC

Vậy EA = EC