Bài 15 trang 45 Toán 9 Tập 2

Bài 4: Công thức nghiệm của phương trình bậc hai

Bài 15 trang 45 Toán 9 Tập 2: Không giải phương trình, hãy xác định các hệ số a, b, c, tính biệt thức Δ và xác định số nghiệm của mỗi phương trình sau:

a) 7x² – 2x + 3 = 0

b) 5x² + 2√10x + 2 =0

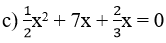
d) 1,7x² – 1,2x – 2,1 = 0

Bài giải:

a) 7x² – 2x + 3 = 0

* Xác định hệ số: a = 7; b = -2; c = 3

* Biệt thức: Δ = b² – 4ac = (-2)² – 4.7.3 = 4 – 84 = -80

* Xác định số nghiệm. Vì Δ < 0 nên phương trình vô nghiệm.

b) 5x² + 2√10x + 2 =0

* Xác định hệ số: a = 5; b = 2√10; c = 2

* Biệt thức: Δ = b² – 4ac = (2√10)² – 4.5.2 = 0

* Xác định số nghiệm: 1 nghiệm kép

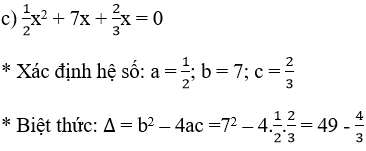
Vậy Δ > 0

* Xác định số nghiệm: phương trình có hai nghiệm phân biệt.

d) 1,7x² – 1,2x – 2,1 = 0

⇔ 17x² – 12x – 21 = 0 (nhân hai vế cho 10)

* Xác định hệ số: a =17; b = -12; c = -21

* Biệt thức: Δ = b² – 4ac = 12² – 4.17.(-21) = 144 + 1428

Vậy Δ > 0

* Xác định số nghiệm: phương trình có hai nghiệm phân biệt.

Chú ý:

1. Để việc tính toán đơn giản hơn, ta đổi các hệ số về số nguyên, nếu được.

2. Tính Δ thật chính xác. Đây là khâu dễ nhầm lẫn nhất.