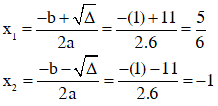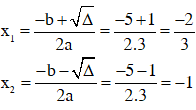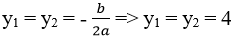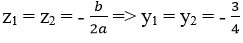Bài 16 trang 45 Toán 9 Tập 2

Bài 4: Công thức nghiệm của phương trình bậc hai

Bài 16 trang 45 Toán 9 Tập 2: Dùng công thức nghiệm của phương trình bậc hai để giải các phương trình sau:

a) 2x² – 7x + 3 = 0         b) 6x² + x = 5 = 0

c) 6x²+ x – 5 = 0         d) 3x² + 5x + 2 = 0

e) y² – 8y + 16 = 0         f) 16z² + 24z + 9 = 0

Bài giải:

Phương pháp:

* Xác định các hệ số

* Tính Δ

* Áp dụng công thức tính nghiệm

a) 2x² – 7x + 3 = 0

* Xác định hệ số: a = 2; b = -7; c = 3

* Tính Δ: Δ = b² – 4ac = (-7)² – 4.2.3 = 49 – 24 = 25

√Δ = 5

* Công thức nghiệm:

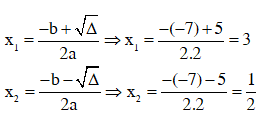
Vậy phương trình có hai nghiệm x = 3 hoặc x = 1/2

Chú ý:

1. Phải thuộc công thức của Δ và công thức tính hai nghiệm

2. Hết sức thận trọng: Δ = 25 ⇒ √Δ=5 (không được viết: √Δ=±5)

b) 6x² + x = 5 = 0

Các hệ số: a = 6; b = 1; c = 5

Biệt số: Δ = b² – 4ac = 1² – 4(6)(5)

Do đó, Δ < 0

Vậy, phương trình vô nghiệm

c) 6x²+ x – 5 = 0

Các hệ số: a = 6; b = 1; c = -5

Biệt thức: Δ = b² – 4ac = 1² – 4(6)(-5) = 121 ⇒ √Δ = 11

Nghiệm

d) 3x² + 5x + 2 = 0

Các hệ số: a = 3; b = 5; c = 2

Biệt thức: Δ = b² – 4ac = 5² – 4.3.2 = 1 ⇒ √Δ = 1

Nghiệm

e) y² – 8y + 16 = 0

Các hệ số: a = 1; b = -8; c = 16

Biệt thức: Δ = b² – 4ac = (-8)² – 4.1.16 = 0

Phương trình có nghiệm kép

f) 16z² + 24z + 9 = 0

Các hệ số: a = 16; b = -24; c = 9

Biệt thức: Δ = b² – 4ac = (-24)² – 4.16.9 = 0

Phương trình có nghiệm kép