Bài 24 trang 111 Toán 9 Tập 1

Luyện tập (trang 111-112)

Bài 24 trang 111 Toán 9 Tập 1: Cho đường tròn (O), dây AB khác đường kính. Qua O kẻ đường vuông góc với AB, cắt tiếp tuyến tại A của đường tròn ở điểm C

a) Chứng minh rằng CB là tiếp tuyến của đường tròn.

b) Cho biết bán kính của đường tròn bằng 15cm, AB = 24cm, Tính độ dài OC.

Bài giải:

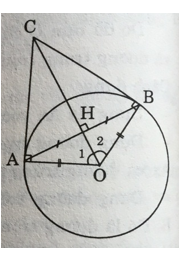
a) CB là tiếp tuyến của đường tròn (O):

Ta chứng minh CB ⊥ OB tại B.

tam giác AOB cân tại O, có OC là đường cao cũng là phân giác

⇒ ∠O₁ = ∠O₂

Xét hai tam giác OAC và OBC có:

OA = OB = bán kính

∠O₁ = ∠O₂ (cmt)

OC chung ⇒ tam giác OAC = tam giác OBC (c.g.c)

⇒ ∠OAC= ∠OBC     (1)

mà ∠OAC = 90° hay CB ⊥ OB tại B.

Vậy CB là tiếp tuyến của đường tròn (O).

b) Độ dài OC, biết R = 15cm, AB = 24 cm.

Gọi H là giao điểm của OC và AB

Do OH ⊥ AB (gt) ⇒ HA = HB = 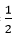AB = 12cm

Áp dụng định lý Pitago vào tam giác vuông OHA: OA² = OH² + HA²

⇒ OH² = OA² - HA² = 15² - 12² = 81 ⇒ OH = 9 (cm)

tam giác OAC vuông tại A, đường cao AH ⇒ OA² = OC.OH

⇒ OC = 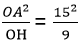= 25cm

Vậy OC = 25 (cm)