Bài 27 trang 88 Toán 9 Tập 1

Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông

Bài 27 trang 88 Toán 9 Tập 1: Giải tam giác vuông ABC vuông tại A biết rằng:

a) b = 10cm; ∠C = 30°;        c) a = 20 cm, ∠B = 35°;

b) c = 10 cm, ∠C = 45°;        d) c = 21cm, b = 18 cm.

Bài giải:

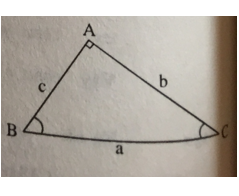
* Nhắc lại: “Giải tam giác vuông” là tìm được tất cả các yếu tố chưa biết của tam giác đó khi ta đã biết trước hai yếu tố (không kể góc vuông) trong đó có ít nhất một yếu tố về cạnh.

a) Biết b = 10 cm, ∠C = 30°. Tính a, c, ∠B?

Áp dụng hệ thức b = a.cosC

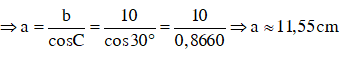
Áp dụng hệ thức c = b.tgC = 10.tg30° = 10.0,9774 = 5,77 cm

Ta có: ∠B + ∠C = 90° ⇒∠B = 90°-∠C = 90° - 30° = 60°

Vậy khi b = 10cm; ∠C = 30° thì: a ≈11,55cm; c = 5,77cm; ∠B = 60°

b) Biết c = 10 cm, ∠C = 45°. Tính a, b, ∠C

Ta có: ∠B + ∠C = 90° ⇒∠B = 90°-∠C = 90° - 45° = 45°

Áp dụng hệ thức b = c.cotgC = 10.cotg45° = 10.1 = 10 cm

Áp dụng hệ thức c = a.sinC

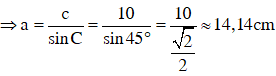
Vậy khi c = 10cm; ∠C = 45° thì: a ≈ 14,18cm; ∠B = 45°; c = 10cm.

Cách khác: góc ∠C = 45° suy ra tam giác ABC vuông cân tại A.

∠B = ∠C= 45°; b = c = 10cm

a = b√2 = 10.1,4142 = 14,14cm

c) Biết a = 20 cm, ∠B = 35°. Tính b, c, ∠C

Ta có: ∠C = 90°-∠B = 90° - 35° = 55°

b = a.sinB= 20.sin35° ≈ 20.0,5736 = 11,47cm

c = a.cosB = 20.cos35° = 20.0,8192 = 16,38 cm

Vậy khi a = 20 cm, ∠B = 35° thì ∠C = 55°, b = 11,47cm, c = 16,38 cm

d) Biết c = 21cm, b = 18cm. Tính góc B, góc C và a.

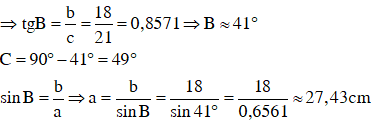
Vậy khi c = 21cm, b = 18cm thì ∠B=41°; ∠C=49°;a ≈27,43cm