Bài 36 trang 94 Toán 9 Tập 1

Ôn tập chương 1

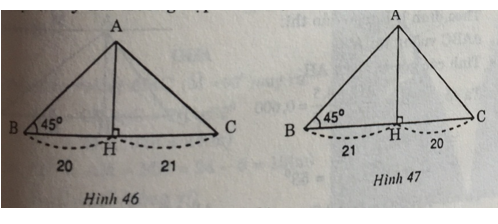
Bài 36 trang 94 Toán 9 Tập 1: Cho tam giác có một góc bằng 45°. Đường cao chia một cạnh kề với góc đó thành các phần 20cm và 21cm. Tìm cạnh lớn trong hai canh còn lại (lưu ý hai trường hợp hình 46, và hình 47).

Bài giải:

* Trường hợp 1 (Hình 46)

Trong tam giác AHB có ∠H = 90° ; ∠B = 45°

⇒ ΔAHB là tam giác vuông cân tại H.

⇒ AH = HB = 20 và AB² = AH² + HB² = 20² + 20² = 800 ⇒ AB = 28 (cm)

Từ tam giác vuông AHC suy ra:

AC² = AH² + HC² = 20² + 21² = 841 ⇒ AC = √841 = 29 (cm)

Vậy độ dài của cạnh lớn trong hai cạnh còn lại là: AC = 29cm

* Trường hợp 2 (hình 47):

Ta có: ∠H = 90° ; ∠B= 45° ⇒ ΔAHB vuông cân tại H.

⇒ AH = HB = 21 và AB2 = AH² + HB² = 21² + 21² = 882 ⇒ AB = √822 = 30 (cm)

AC² = AH² + HC² = 21² + 20² = 841 ⇒ AC = √841= 29(cm)

Vậy độ dài của cạnh lớn trong hai cạnh còn lại là: AB = 30(cm).