Bài 37 trang 94 Toán 9 Tập 1

Ôn tập chương 1

Bài 37 trang 94 Toán 9 Tập 1: Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7, 5cm.

a) Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó.

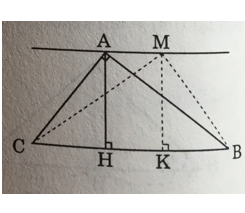
b) Hỏi rằng điểm M mà diện tích tam giác MBC bằng diện tích tam giác ABC nằm trên đường nào?

Bài giải:

a) ΔABC vuông tại A.

Ta có: BC² = (7,5)² = 56,25         (1)

AB² + AC² = 6² + (4,5)² = 56,25         (2)

Từ (1) và (2) suy ra:

BC² = AB² + AC²

Theo định lí Pitago đảo thì: ΔABC vuông tại A

Tính các góc B, C và AH

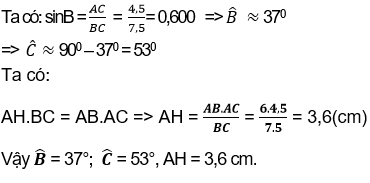
b) Xác định vi trí của M

Gọi MK là đường cao kẻ từ M của ΔMBC, ta có: