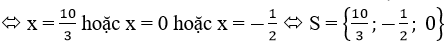Bài 39 trang 57 Toán 9 Tập 2

Luyện tập (trang 56-57)

Bài 39 trang 57 Toán 9 Tập 2: Giải phương trình bằng cách đưa về phương trình tích:

a) (3x² – 7x – 10)[2x²+(1-√5)x+√5-3] = 0

b) x³ + 3x² – 2x – 6 = 0;

c) (x² – 1)(0,6x + 1) = 0,6x² + x;

d) (x² + 2x – 5)² = (x² – x +5)².

Bài giải:

a) (3x² – 7x – 10)[2x²+(1-√5)x+√5-3] = 0

⇔ 3x² – 7x – 10 = 0 hoặc 2x²+(1-√5)x+√5-3 = 0

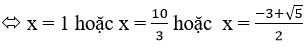
b) x³ + 3x² – 2x – 6 = 0

⇔ (x + 3)(x²) – 2x(x + 3) = 0

⇔ x = -3 hoặc x = ±√2 ⇔ S = {-3; ±√2}

c) (x² – 1)(0,6x + 1) = 0,6x² + x

⇔ (x² – 1)(0,6x + 1) – (0,6x + 1)x = 0

⇔ (0,6x +1)(x² – x – 1) = 0

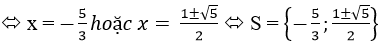
d) (x² + 2x – 5)² = (x² – x +5)²

⇔ x² + 2x – 5 = x² – x +5 hoặc x² + 2x – 5 = -(x² – x +5)