Bài 70 trang 95 Toán 9 Tập 2

Luyện tập (trang 95-96)

Bài 70 trang 95 Toán 9 Tập 2: Vẽ lại ba hình dưới đây và tính chu vi của mỗi hình (có gạch chéo):

Bài giải:

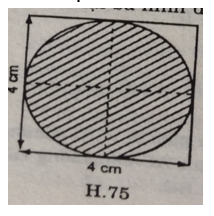
* Hình 75: Hình có gạch chéo là một hình tròn nội tiếp hình vuông cạnh 4cm. Đường kính của đường tròn bằng cạnh hình vuông (4cm)

Do đó chu vi của hình có gạch chéo là: C = πd = 3,14.4 = 12,56 (cm)

(Học sinh tự chứng minh đường kính hình tròn bằng cạnh hình vuông)

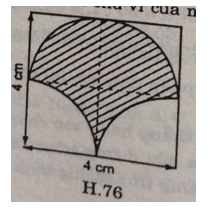
* Hình 76: Ta có MN và KI là hai trục đối xứng của hình vuông ABCD, cũng là trục đối xứng của hình tròn (O).

⇒ sđ cung MK = sđ cung KN = sđ cung NI = sđ cung IM (cùng bằng 1/4 độ dài của đường tròn có bán kính 2cm)

⇒ Chu vi của hình có gạch chéo bằng chu vi của đường tròn có bán kính 2cm và bằng 2.3,14.2 = 12,56 (cm)

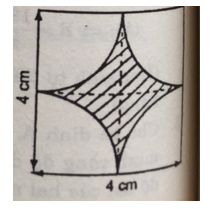
* Hình 79:

Chứng minh tương tự trên, ta có chu vi của hình có gạch chéo trong hình 54 bằng chu vi một đường tròn có bán kính 2cm bằng 12,56cm.

Lưu ý: Các hình có gạch chéo trong ba hình đã cho tuy không giống nhau nhưng chu vi của chung bằng nhau và bằng chu vi của một đường tròn có bán kính 2cm.

Ngoài cách tính trên, ta có thể tính độ dài của một cung tròn có số đo 90° thuộc đường tròn bán kính 2cm rồi lấy kết quả nhân với 4 ta sẽ có chu vi của hình gạch chéo.