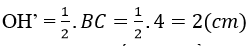Bài 77 trang 98 Toán 9 Tập 2

Bài 10: Diện tích hình tròn, hình quạt tròn

Bài 77 trang 98 Toán 9 Tập 2: Tính diện tích hình tròn nội tiếp một hình vuông có cạnh là 4cm.

Bài giải:

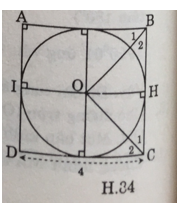
Gọi ABCD là hình vuông có cạnh 4cm.

O là tâm đường tròn nội tiếp ABCD

H và I là các tiếp điểm của BC và AD và (O)

⇒ OH ⊥ BC và OI⊥ AD (tiếp tuyến vuông góc với bán kính đi qua tiếp điểm).

Mà BC // AD ⇒ I, O, H thẳng hàng ⇒ IH là đường kính của (O). Tứ giác ABHI là hình chữ nhật.

⇒ IH = AB = 4cm

⇒ OH = OI = 2cm

⇒ S(O) = π.OH² = π.2² = 3,14.4 = 12,56 (cm²)

Vậy diện tích của hình tròn (O) nội tiếp hình vuông cạnh 4cm là: 12, 56cm².

* Ghi chú: Ta có thể tính OH bằng cách khác. Theo tính chất hai tiếp tuyến cắt nhau ta có:

Góc B₁ = góc B₂ = 45° và góc C₁ = góc C₂ = 45°

⇒ ΔBOC vuông cân tại O có OH là đường cao cũng là trung tuyến nên