Hãy xác định trọng tâm của một bản mỏng, đồng chất, hình chữ nhật, dài 12cm, rộng 6cm

Bài 28: Quy tắc hợp lực song song. Điều kiện cân bằng của một vật rắn dưới tác dụng của ba lực song song

Bài 1 (trang 131 sgk Vật Lý 10 nâng cao): Hãy xác định trọng tâm của một bản mỏng, đồng chất, hình chữ nhật, dài 12cm, rộng 6cm, bị cắt mất một mẩu hình vuông có cạnh 3cm (hình 28.10).

Lời giải:

Ta coi bản phẳng coi như gồm hai bản AHEF và HBCD ghép lại.

Biểu diễn trọng tâm các bản như hình vẽ sau:

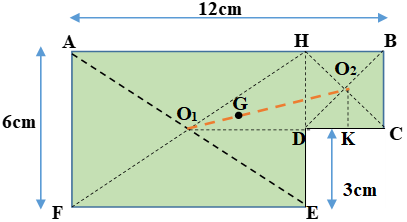
Phần hình chữ nhật AHEF có trọng lực P₁→ đặt tại tâm đối xứng O₁.

Phần hình vuông HBCD có trọng lực P₂→ đặt tại tâm đối xứng O₂.

Hợp lực của hai lực P₁→và P₂→là P→phải có điểm đặt tại G nằm trên đoạn thẳng O₁O₂. Gọi G chính là trọng tâm của cả bản phẳng.

Vì các bản đồng chất, phẳng mỏng đều nên tỉ lệ diện tích bằng tỉ lệ về trọng lượng:

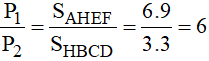
Ta có:

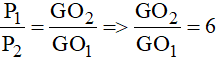
⇔ 6GO₁ - GO₂ = 0 (1)

Xét tam giác vuông O₁O₂K ta có:

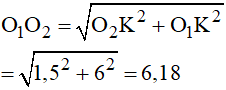
⇔ GO₁ + GO₂ = 6,18 (2)

Giải hệ (1), (2) ta được GO₁ ≈ 0,88cm.

Vậy trọng tâm G của bản phẳng nằm trên đoạn O₁O₂, cách O₁ một đoạn 0,88cm.