Parabol nhận trục tung làm trục đối xứng và cắt đường thẳng y = x/2 tại các điểm có hoành độ là -1 và 3/2

Ôn tập cuối năm

Bài 1 trang 211 Sách bài tập Đại số 10: Xác định parabol y = ax² + bx + c trong mỗi trường hợp sau

    a) Parabol nhận trục tung làm trục đối xứng và cắt đường thẳng y = x/2 tại các điểm có hoành độ là -1 và 3/2

    b) Parabol đi qua gốc tọa độ và có đỉnh là điểm (1;2).

    c) Parabol đi qua hai điểm A(-1; 2), B(2; 3) và có trục đối xứng là đường thẳng x = 1.

Lời giải:

    a) Vì đồ thị nhận trục tung làm trục đối xứng cho nên hàm số f(x) = ax² + bx + c là hàm số chẵn, do đó

    f(x) = ax² + bx + c = ax² - bx + c = f(-x), ∀x

    Suy ra b = 0. Ta còn phải xác định a và c.Suy ra b = 0. Ta còn phải xác định a và c.

    Vì parabol cắt đường thẳng y = x/2 tại các điểm có hoành độ -1 và 3/2 nên nó đi qua các điểm (-1; -1/2) và (3/2; 3/4)

    Ta có hệ phương trình

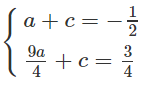
    Giải hệ phương trình trên ta được a = 1; c = -3/2

    Parabol phải tìm là y = x² - 3/2

    b) Vì parabol đi qua (0;0) nên y(0) = c = 0.

    Do parabol có đỉnh là (1 ; 2) nên

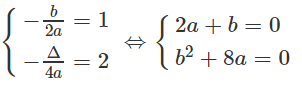
    Giải hệ phương trình trên ta được a = -2, b = 4.

    Parabol phải tìm là y = -2x² + 4x

    c) a = -1/3, b = 2/3, c = 3